If you like Skforecast , help us giving a star on GitHub! ⭐️
Forecasting electricity demand with Python
- Skforecast: time series forecasting with Python and Scikit-learn
- Forecasting web traffic with machine learning and Python
- Forecasting time series with gradient boosting: Skforecast, XGBoost, LightGBM and CatBoost
- Bitcoin price prediction with Python, when the past does not repeat itself
- Prediction intervals in forecasting models
- Multi-series forecasting
- Reducing the influence of Covid-19 on time series forecasting models
- Forecasting time series with missing values
- Intermittent demand forecasting
Introduction¶
A time series is a sequence of chronologically ordered data at equal or unequal intervals. The forecasting process consists of predicting the future value of a time series, either by modelling the series solely on the basis of its past behavior (autoregressive) or by using other external variables.
When working with time series, it is rarely necessary to predict only the next element in the series ($t_{+1}$). Instead, the most common goal is to forecast a whole future interval (($t_{+1}$), ..., ($t_{+n}$)) or a far future time ($t_{+n}$). Several strategies can be used to generate this type of forecast, skforecast has implemented the following for univariate time series forecasting:
Recursive multi-step forecasting: since the value $t_{n-1}$ is needed to predict $t_{n}$, and $t_{n-1}$ is unknown, a recursive process is applied in which, each new prediction, is based on the previous one. This process is known as recursive forecasting or recursive multi-step forecasting and can be easily generated with the
ForecasterAutoregandForecasterAutoregCustomclasses.Direct multi-step forecasting: this method consists of training a different model for each step of the forecast horizon. For example, to predict the next 5 values of a time series, 5 different models are trained, one for each step. As a result, the predictions are independent of each other. This entire process is automated in the
ForecasterAutoregDirectclass.
This document shows an example of how to use forecasting methods to predict hourly electricity demand. Specifically, it introduces skforecast, a simple library that contains the classes and functions necessary to adapt any scikit-learn regression model to forecasting problems.
More examples in skforecast-examples.
Use Case¶
A time series of electricity demand (MW) is available for the state of Victoria (Australia) from 2011-12-31 to 2014-12-31 is available. It is intended to generate a forecasting model capable of predicting the next day's energy demand at the hourly level.
# Data manipulation
# ==============================================================================
import numpy as np
import pandas as pd
# Plots
# ==============================================================================
import matplotlib.pyplot as plt
import seaborn as sns
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.graphics.tsaplots import plot_pacf
plt.style.use('seaborn-v0_8-darkgrid')
# Modelling and Forecasting
# ==============================================================================
from sklearn.linear_model import Ridge
from lightgbm import LGBMRegressor
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import mean_absolute_error
from skforecast.ForecasterAutoreg import ForecasterAutoreg
from skforecast.ForecasterAutoregDirect import ForecasterAutoregDirect
from skforecast.model_selection import grid_search_forecaster
from skforecast.model_selection import backtesting_forecaster
from sklearn.preprocessing import OneHotEncoder
from sklearn.compose import make_column_transformer
from sklearn.compose import make_column_selector
# Warnings configuration
# ==============================================================================
import warnings
warnings.filterwarnings('once')
Data¶
The data used in this document has been obtained from the R tsibbledata package. The dataset contains 5 columns and 52,608 complete records. The information in each column is:
Time: date and time of the record.
Date: date of the record.
Demand: electricity demand (MW).
Temperature: temperature in Melbourne, the capital of Victoria.
Holiday: indicates if the day is a public holiday.
# Data download
# ==============================================================================
url = ('https://raw.githubusercontent.com/JoaquinAmatRodrigo/skforecast/master/' +
'data/vic_elec.csv')
data = pd.read_csv(url, sep=',')
data.info()
The Time column is stored as a string. To convert it to datetime, the function pd.to_datetime() is used. Once in datetime format, and to make use of pandas functionalities, it is set as an index. Since the data was recorded every 30 minutes, the frequency ('30min') is also specified.
# Data preparation
# ==============================================================================
data = data.copy()
data['Time'] = pd.to_datetime(data['Time'], format='%Y-%m-%dT%H:%M:%SZ')
data = data.set_index('Time')
data = data.asfreq('30min')
data = data.sort_index()
data.head(2)
One of the first analyses to be carried out when working with time series is to check that the series is complete.
# Verify that a temporary index is complete
# ==============================================================================
(data.index == pd.date_range(start=data.index.min(),
end=data.index.max(),
freq=data.index.freq)).all()
print(f"Number of rows with missing values: {data.isnull().any(axis=1).mean()}")
# Fill gaps in a temporary index
# ==============================================================================
# data.asfreq(freq='30min', fill_value=np.nan)
Although the data is at 30 minute intervals, the aim is to create a model capable of predicting hourly electricity demand, so the data needs to be aggregated. This type of transformation can be done very quickly by combining the Pandas time type index and its resample() method.
It is very important to use the closed='left' and label='right' arguments correctly to avoid introducing future information into the training, leakage). Suppose that values are available for 10:10, 10:30, 10:45, 11:00, 11:12, and 11:30. To obtain the hourly average, the value assigned to 11:00 must be calculated using the values for 10:10, 10:30, and 10:45; and the value assigned to 12:00 must be calculated using the value for 11:00, 11:12 and 11:30.
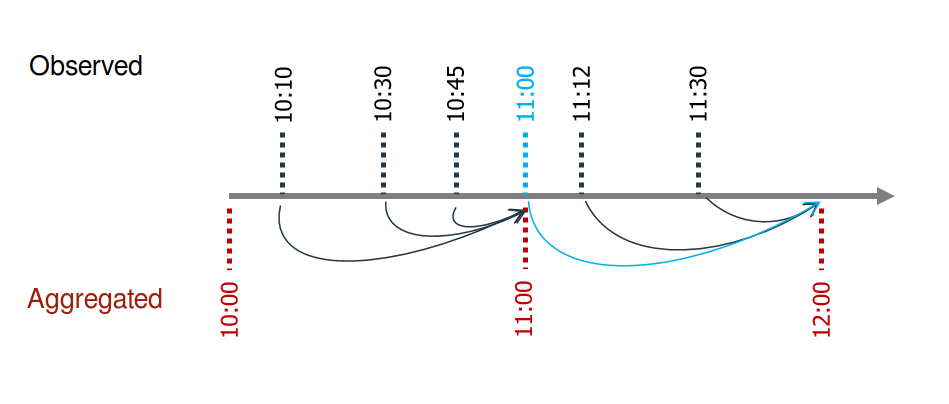
The 11:00 average does not include the 11:00 point value because in reality the value is not available at that exact time.
# Aggregating in 1H intervals
# ==============================================================================
# The Date column is eliminated so that it does not generate an error when aggregating.
# The Holiday column does not generate an error since it is Boolean and is treated as 0-1.
data = data.drop(columns='Date')
data = data.resample(rule='H', closed='left', label ='right').mean()
data
The dataset starts on 2011-12-31 14:00:00 and ends on 2014-12-31 13:00:00. The first 10 and the last 13 records are discarded so that it starts on 2012-01-01 00:00:00 and ends on 2014-12-30 23:00:00. In addition, in order to optimize the hyperparameters of the model and evaluate its predictive ability, the data is divided into 3 sets, training, validation and test.
# Split data into train-val-test
# ==============================================================================
data = data.loc['2012-01-01 00:00:00': '2014-12-30 23:00:00'].copy()
end_train = '2013-12-31 23:59:00'
end_validation = '2014-11-30 23:59:00'
data_train = data.loc[: end_train, :].copy()
data_val = data.loc[end_train:end_validation, :].copy()
data_test = data.loc[end_validation:, :].copy()
print(f"Train dates : {data_train.index.min()} --- {data_train.index.max()} (n={len(data_train)})")
print(f"Validation dates : {data_val.index.min()} --- {data_val.index.max()} (n={len(data_val)})")
print(f"Test dates : {data_test.index.min()} --- {data_test.index.max()} (n={len(data_test)})")
Graphic exploration¶
When building a forecasting model, it may be useful to plot the time series values. This allows patterns such as trends and seasonality to be identified.
Full time series
# Time series plot
# ==============================================================================
fig, ax = plt.subplots(figsize=(8, 3.5))
data_train.Demand.plot(ax=ax, label='train', linewidth=1)
data_val.Demand.plot(ax=ax, label='validation', linewidth=1)
data_test.Demand.plot(ax=ax, label='test', linewidth=1)
ax.set_title('Electricity demand')
ax.legend();
The graph above shows that electricity demand has an annual seasonality. There is a peak in July and very pronounced peaks in demand between January and March.
Section of the time series
Due to the variance of the time series, it is not possible to see the possible intraday pattern from a single chart.
# Zooming time series chart
# ==============================================================================
zoom = ('2013-05-01 14:00:00','2013-06-01 14:00:00')
fig = plt.figure(figsize=(8, 4))
grid = plt.GridSpec(nrows=8, ncols=1, hspace=0.6, wspace=0)
main_ax = fig.add_subplot(grid[1:3, :])
zoom_ax = fig.add_subplot(grid[5:, :])
data.Demand.plot(ax=main_ax, c='black', alpha=0.5, linewidth=0.5)
min_y = min(data.Demand)
max_y = max(data.Demand)
main_ax.fill_between(zoom, min_y, max_y, facecolor='blue', alpha=0.5, zorder=0)
main_ax.set_xlabel('')
data.loc[zoom[0]: zoom[1]].Demand.plot(ax=zoom_ax, color='blue', linewidth=1)
main_ax.set_title(f'Electricity demand: {data.index.min()}, {data.index.max()}', fontsize=10)
zoom_ax.set_title(f'Electricity demand: {zoom}', fontsize=10)
zoom_ax.set_xlabel('')
plt.subplots_adjust(hspace=1)
When the time series are zoomed in, a clear weekly seasonality can be seen, with higher consumption during the working week (Monday to Friday) and lower consumption at weekends. There is also a clear correlation between the consumption of one day and that of the previous day.
Annual, weekly and daily seasonality
# Boxplot for annual seasonality
# ==============================================================================
fig, ax = plt.subplots(figsize=(7, 2.5))
data['month'] = data.index.month
data.boxplot(column='Demand', by='month', ax=ax,)
data.groupby('month')['Demand'].median().plot(style='o-', linewidth=0.8, ax=ax)
ax.set_ylabel('Demand')
ax.set_title('Demand distribution by month')
fig.suptitle('');
It is observed that there is an annual seasonality, with higher (median) demand values in June, July, and August, and with high demand peaks in November, December, January, February, and March.
# Boxplot for weekly seasonality
# ==============================================================================
fig, ax = plt.subplots(figsize=(7, 2.5))
data['week_day'] = data.index.day_of_week + 1
data.boxplot(column='Demand', by='week_day', ax=ax)
data.groupby('week_day')['Demand'].median().plot(style='o-', linewidth=0.8, ax=ax)
ax.set_ylabel('Demand')
ax.set_title('Demand distribution by week day')
fig.suptitle('');
Weekly seasonality shows lower demand values during the weekend.
# Boxplot for daily seasonality
# ==============================================================================
fig, ax = plt.subplots(figsize=(7, 2.5))
data['hour_day'] = data.index.hour + 1
data.boxplot(column='Demand', by='hour_day', ax=ax)
data.groupby('hour_day')['Demand'].median().plot(style='o-', linewidth=0.8, ax=ax)
ax.set_ylabel('Demand')
ax.set_title('Demand distribution by the time of the day')
fig.suptitle('');
There is also a daily seasonality, with demand falling between 16:00 and 21:00 hours.
Holidays and non-holiday days
# Violinplot
# ==============================================================================
fig, ax = plt.subplots(figsize=(6, 3))
sns.violinplot(
x = 'Demand',
y = 'Holiday',
data = data.assign(Holiday = data.Holiday.astype(str)),
palette = 'tab10',
ax = ax
)
ax.set_title('Distribution of demand between holidays and non-holidays')
ax.set_xlabel('Demand')
ax.set_ylabel('Holiday');
Consumption tends to be lower on public holidays.
Autocorrelation plots
# Autocorrelation plot
# ==============================================================================
fig, ax = plt.subplots(figsize=(5, 2))
plot_acf(data.Demand, ax=ax, lags=60)
plt.show()
# Partial autocorrelation plot
# ==============================================================================
fig, ax = plt.subplots(figsize=(5, 2))
plot_pacf(data.Demand, ax=ax, lags=60)
plt.show()
The autocorrelation and partial autocorrelation plots show a clear relationship between demand in one hour and the previous hours, and between demand in one hour and the same hour in previous days. This type of correlation is an indication that autoregressive models can work well.
Recursive multi-step forecasting¶
A recursive autoregressive model (ForecasterAutoreg) is created and trained from a linear regression model with a Ridge penalty and a time window of 24 lags. This means that for each prediction, the demand values of the previous 24 hours are used as predictors.
Forecaster training¶
A StandardScaler is used as data pre-processing transformation.
# Create and train forecaster
# ==============================================================================
forecaster = ForecasterAutoreg(
regressor = Ridge(random_state=123),
lags = 24,
transformer_y = StandardScaler()
)
forecaster.fit(y=data.loc[:end_validation, 'Demand'])
forecaster
Backtest¶
It evaluates how the model would have behaved if it had been trained on data from 2012-01-01 00:00 to 2014-11-30 23:59 and then every day at 23:59 it predicted the next 24 hours. This type of evaluation, known as backtesting, can be easily implemented with the function backtesting_forecaster(). This function returns an error metric in addition to the predictions.
# Backtest
# ==============================================================================
metric, predictions = backtesting_forecaster(
forecaster = forecaster,
y = data['Demand'],
steps = 24,
metric = 'mean_absolute_error',
initial_train_size = len(data.loc[:end_validation]),
refit = False,
verbose = True,
show_progress = True
)
# Plot
# ==============================================================================
fig, ax = plt.subplots(figsize=(8, 3.5))
data.loc[predictions.index, 'Demand'].plot(ax=ax, linewidth=2, label='real')
predictions.plot(linewidth=2, label='prediction', ax=ax)
ax.set_title('Prediction vs real demand')
ax.legend();
# Backtest error
# ==============================================================================
print(f'Backtest error: {metric}')
Hyperparameter tuning¶
The trained ForecasterAutoreg object used the first 24 lags and a Ridge model with the default hyperparameters. However, there is no reason why these values are the most appropriate.
To identify the best combination of lags and hyperparameters, a Grid Search with validation by Backtesting is used. This process consists of training a model with different combinations of hyperparameters and lags and evaluating its predictive capacity. In the search process, it is important to evaluate the models using only the validation data and not to include the test data, which is only used to evaluate the final model.
# Hyperparameter Grid search
# ==============================================================================
forecaster = ForecasterAutoreg(
regressor = Ridge(random_state=123),
lags = 24, # This value will be replaced in the grid search
transformer_y = StandardScaler()
)
# Lags used as predictors
lags_grid = [5, 24, [1, 2, 3, 23, 24, 25, 47, 48, 49]]
# Regressor's hyperparameters
param_grid = {'alpha': np.logspace(-3, 5, 10)}
results_grid = grid_search_forecaster(
forecaster = forecaster,
y = data.loc[:end_validation, 'Demand'],
steps = 24,
metric = 'mean_absolute_error',
param_grid = param_grid,
lags_grid = lags_grid,
initial_train_size = len(data[:end_train]),
refit = False,
return_best = True,
verbose = False
)
# Grid Search results
# ==============================================================================
results_grid
The best results are obtained by using the lags [1, 2, 3, 23, 24, 25, 47, 48, 49] and a Ridge configuration {'alpha': 215.44}. By specifying return_best = True in the grid_search_forecaster() function. The forecaster object is automatically retrained at the end of the process with the best configuration found and the full dataset (train + validation).
forecaster
Backtest with test data¶
Once the best model has been identified and trained, its error in predicting the test data is calculated.
# Backtest final model
# ==============================================================================
metric, predictions = backtesting_forecaster(
forecaster = forecaster,
y = data['Demand'],
steps = 24,
metric = mean_absolute_error,
initial_train_size = len(data[:end_validation]),
refit = False,
verbose = False,
show_progress = True
)
fig, ax = plt.subplots(figsize=(8, 3.5))
data.loc[predictions.index, 'Demand'].plot(linewidth=2, label='real', ax=ax)
predictions.plot(linewidth=2, label='prediction', ax=ax)
ax.set_title('Prediction vs real demand')
ax.legend();
# Backtest error
# ==============================================================================
print(f'Backtest error: {metric}')
After optimization of lags and hyperparameters, the prediction error was reduced from 289.5 to 251.9.
Prediction intervals¶
A prediction interval defines the interval within which the true value of "y" can be expected to be found with a given probability.
Rob J Hyndman and George Athanasopoulos, in their book Forecasting: Principles and Practice, list multiple ways to estimate prediction intervals, most of which require that the residuals (errors) of the model to be normally distributed. If this cannot be assumed, one can resort to bootstrapping, which requires only that the residuals are uncorrelated. This is the method used in the skforecast library.
# Backtest with test data and intervals
# ==============================================================================
metric, predictions = backtesting_forecaster(
forecaster = forecaster,
y = data['Demand'],
steps = 24,
metric = 'mean_absolute_error',
initial_train_size = len(data.loc[:end_validation]),
refit = False,
interval = [10, 90],
n_boot = 500,
in_sample_residuals = True,
verbose = False,
show_progress = True
)
print('Backtesting metric:', metric)
predictions.head(5)
# Plot
# ==============================================================================
fig, ax = plt.subplots(figsize=(8, 3.5))
data.loc[predictions.index, 'Demand'].plot(linewidth=2, label='real', ax=ax)
predictions.iloc[:, 0].plot(linewidth=2, label='prediction', ax=ax)
ax.set_title('Prediction vs real demand')
ax.fill_between(
predictions.index,
predictions.iloc[:, 1],
predictions.iloc[:, 2],
alpha = 0.4,
color = 'orange',
label = 'prediction interval'
)
ax.legend();