Introducción a grafos y redes con Python

Introducción a grafos y redes con Python

Fernando Carazo, Joaquín Amat
Febrero, 2023

Más sobre ciencia de datos: cienciadedatos.net

Introducción


Una de las últimas tendencias en el campo de la inteligencia artificial es el Graph Machine Learning (GML). Esta disciplina se centra en aplicar algoritmos de machine learning y estadística al estudio de redes o grafos complejos.

Un grafo es una estructura de datos formada por nodos y enlaces que permite representar relaciones entre objetos. A modo de ejemplo, en una red social, los nodos podrían representar a los usuarios y los enlaces la conexión entre ellos.

El GML utiliza grafos para entrenar modelos de aprendizaje automático y poder hacer inferencia sobre los nodos o enlaces. Los tres tipos principales de problemas que se pueden resolver con GML son:

  • Inferencia sobre nodos: predecir características de los nodos utilizando las características de sus nodos vecinos.

  • Inferencia sobre enlaces: predecir carteristicas o exitencia de enlaces, por ejemplo, inferir qué enlaces tiene mayor probabilidad de ocurrir en un futuro. Este es un caso típico de los sistemas de recomendación.

  • Inferencia sobre conjuntos de nodos: identificar comunidades de nodos que presentan comportamientos similares. Este es un caso típico en segmentación de clientes con características similares.

En esta serie de artículos se pretende mostrar las bases del Graph Machine Learning y resolver casos prácticos utilizando las librerías de grafos más importantes de Python como NetworkX PyTorch Geometric, Stellargraph o Graph Neural Networks.


Mapa parcial de internet basado en la información obtenida del sitio opte.org el 15 de enero de 2005. Cada linea dibujada entre dos nodos representa el enlace entre dos direcciones IP. La longitud de las líneas es proporcional al tiempo de espera entre los nodos. La imagen representa 30% de las redes accesibles en el año 2005.

Tipos de grafos


Los grafos se clasifican en base a sus nodos y los enlaces. Se pueden diferenciar varios tipos de grafos dependiendo del tipo de relación que existe entre sus nodos.

Grafos no dirigidos

Los enlaces no tienen dirección, es decir, si un nodo $A$ está conectado a un nodo $B$, entonces $B$ también está conectado a $A$. Un ejemplo de grafo no dirigido es una red social donde los usuarios están conectados entre sí a través de vínculos de amistad.

Ejemplo de un red social, donde los nodos son usuarios y los ejes indican si existe una relación de amistad entre ellos. Es un grafo no dirigido porque las conexiones no tienen direccionalidad.


Grafos dirigidos

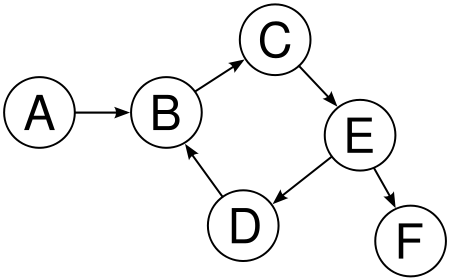
Los enlaces tienen una dirección, es decir, si un nodo $A$ está conectado a un nodo $B$, $B$ no está necesariamente conectado a $A$. Un ejemplo de un grafo dirigido es una red de llamadas telefónicas donde los nodos son personas y los ejes muestran cada llamada, teniendo en cuenta quién llama a quién.


Ejemplo de grafo dirigido.

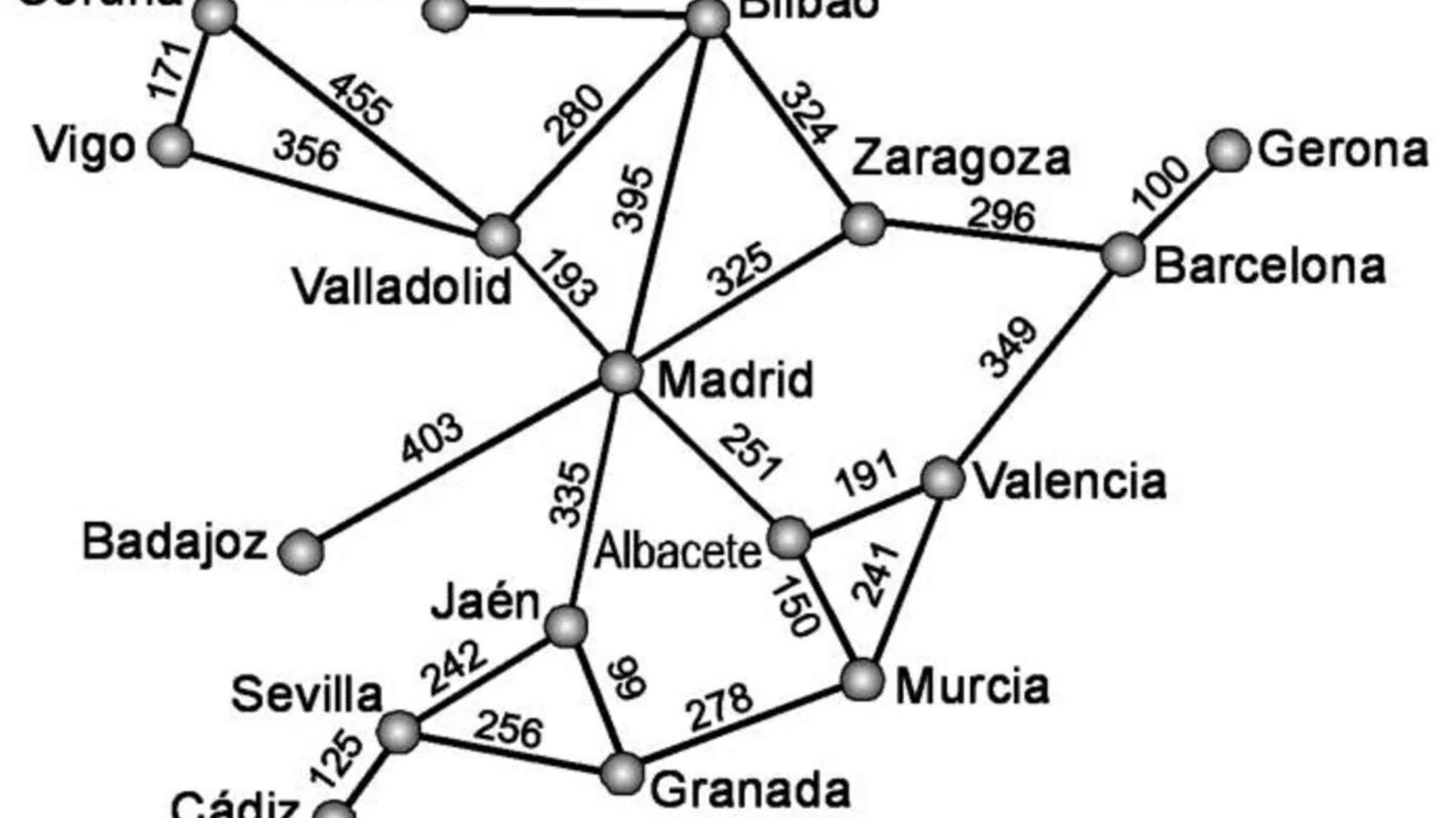
**Grafos ponderados** Los enlaces tienen un peso asociado, que representa la importancia o la intensidad de la relación entre los nodos. Un ejemplo de grafo ponderado es una red de ciudades donde los enlaces representan las rutas de transporte y el peso representa la distancia entre ciudades.


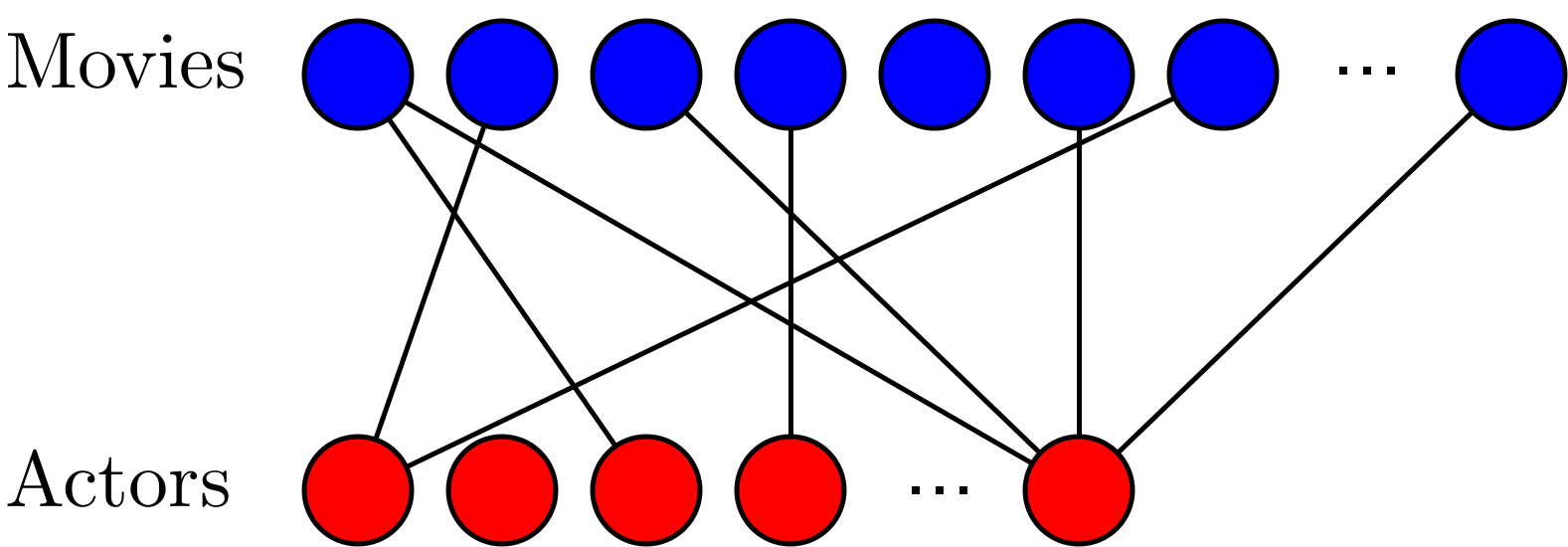
Ejemplo de un red de ciudades, donde los nodos son ciudades y los ejes la distancia entre ellas. Es un grafo ponderado.


Grafos bipartitos

Los nodos se dividen en dos conjuntos disjuntos (dos tipos de nodos), y solo se permiten enlaces entre nodos de diferentes conjuntos. Un ejemplo de grafo bipartito es una red de películas y actores, donde los nodos de un conjunto son las películas y los nodos del otro conjunto son los actores; y solo se permiten enlaces entre películas y actores.


Ejemplo de un grafo bipartito, donde los nodos pueden ser de dos tipos: actores o películas.

Matriz de adyacencia


Para poder analizar un grafo es neceario representarlo de forma matemática. Existen dos formas principales de hacerlo: la lista de ejes (edgelist) y la matriz de adyacencia.

La lista de ejes es simplemente una lista en la que se indican todas las conexiones. Por ejemplo, en un grafo dirigido con tres nodos {$A$, $B$ y $C$}, donde $A$ se conecta con $B$ y $C$, la lista de ejes es {($A$,$B$), ($A$,$C$)}. Si el grafo es no dirigido, la lista debe incluir las conexiones en ambas direcciones {($A$,$B$), ($B$,$A$) ($A$,$C$), ($C$,$A$)}.

Otra forma de representar un grafo es mediante lo que se conoce como matriz de adyacencia. La matriz de adyacencia es una matriz de dimensión $NxN$, siendo $N$ el número de nodos y donde aparece un 1 si la conexión entre un par de nodos existe y un 0 de lo contrario. Para grafos ponderados, en vez de un 1, la matriz presenta el valor del peso de la conexión. Debido a sus propiedades matemáticas, la matriz de adyacencia es el método de representación de grafos más utilizado.

La desventaja de la matriz de adyacencia, es que para grafos muy grandes, puede ocupar mucho espacio. Por este motivo, se utiliza con frecuencia una matriz de adyacencia sparse, que internamente únicamente almacena la información de las conexiones existentes, es decir, no almacena los ceros.

Para grafos no dirigidos la matriz de adyacencia es simétrica ya que, si existe la conexión entre los nodos $A$ y $B$, también existirá la conexión recíproca.

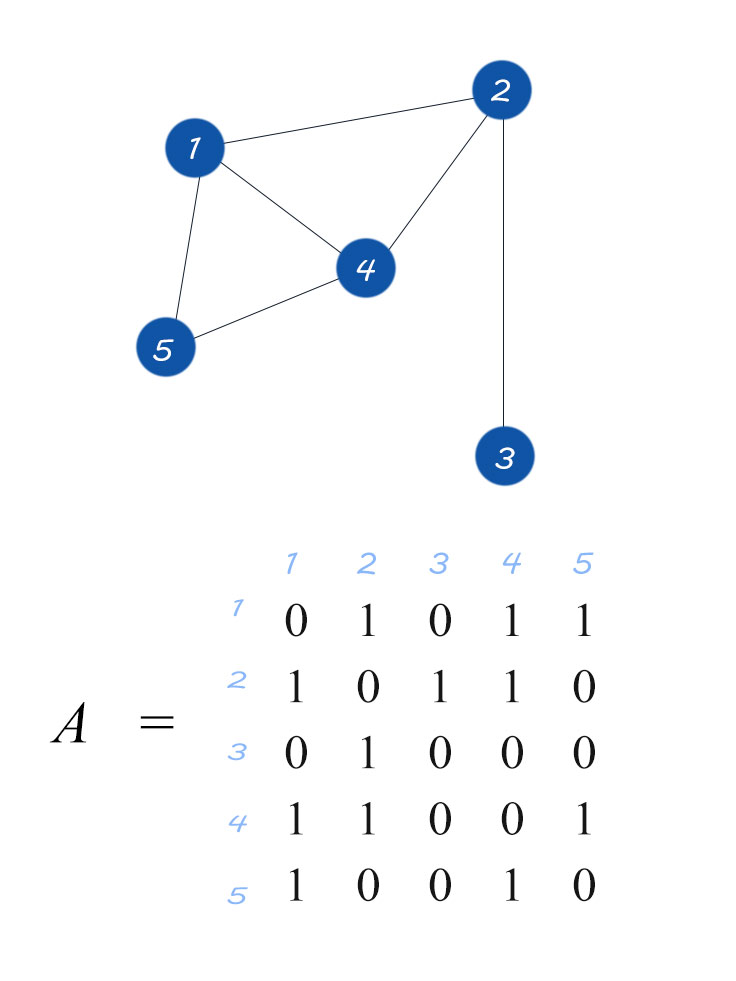
Ejemplo de un grafo y su matriz de adyacencia. Al ser un grafo no dirigido, la matriz es simétrica.


Con una formulación matetemática, la matriz de adyacencia de un grafo dirigido de $\mathrm{N}$ nodos tiene $\mathrm{N}$ filas y $\mathrm{N}$ columnas, siendo sus elementos:

  • $A_{i j}=1$ si existe un enlace que apunta desde el nodo $j$ al nodo $i$

  • $A_{i j}=0$ si los nodos $i$ y $j$ no están conectados entre sí

La matriz de adyacencia de una red no dirigida tiene dos entradas para cada enlace. El enlace $(1,2)$ se representa como $A_{12}$ $=1$ y $A_{21}=1$. Por lo tanto, la matriz de adyacencia de una red no dirigida es simétrica, $A_{i j}=A_{j i}.$

En la siguiente figura se representan los distintos tipos de grafos junto con sus matrices de adyacencia. Como se puede observar, los grafos dirigidos ($B$) son los únicos que no tienen una matriz de adyacencia simétrica. En el caso de los grafos bipartitos ($D$), se pueden proyectar para obtener las conexiones indirectas entre cada tipo de nodo ($E$), esto último se verá en profundidad más adelante.


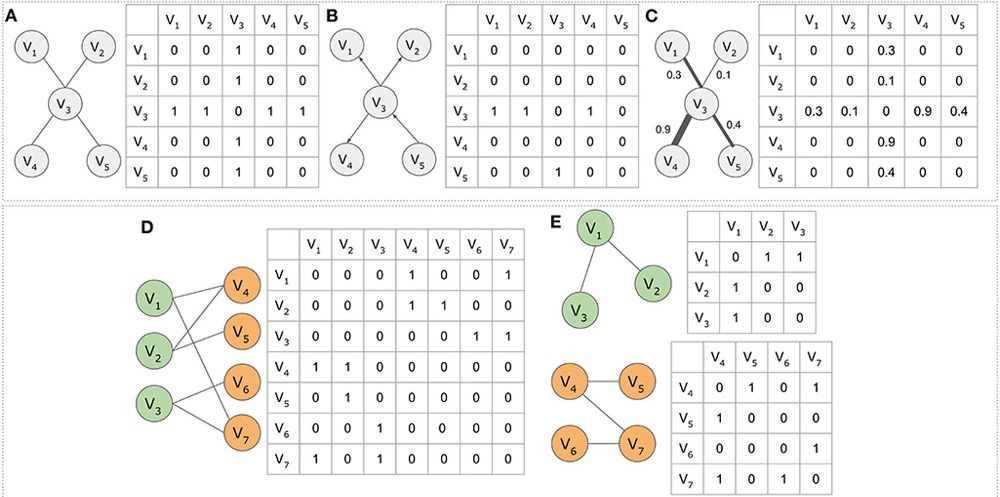
Ejemplo de grafos de distintos tipos con sus matrices de adyacencia correspondientes. A) Grafo no dirigido. B) Grafo dirigido. C) Grafo ponderado. D) Grafo bipartito, con dos tipos de nodos (verde y naranja). E) Proyección del grafo bipartito en los nodos de cada tipo. Fuente: wikipedia.

Meta-información de nodos y ejes.


Cuando se trabaja con grafos, especialmente si se quieren hacer predicciones u otro tipo de analítica, es muy común que se disponga de información adicional de los nodos y enlaces. Esta información se denomina meta-información porque no pertenece estrictamente al grafo y se suele almacenar a modo de tabla, cuyas filas son los nodos o enlaces y sus columnas son las variables disponibles de cada uno. Si se utiliza el ejemplo de la red social, la meta-información de los nodos podría ser el nombre, edad, aficiones, etc...

Aunque menos común que para los nodos, los enlaces también pueden tener meta-información. Continuando con el ejmplo de la red social, la meta-información de los ejes podría ser el año en el que se inició la relación de amistad entre dos personas.

Grafos bipartitos


Un grafo bipartito es una red cuyos nodos se pueden dividir en dos conjuntos disjuntos $U$ y $V$ de tal manera que los enlaces conectan nodos de $U$ con nodos de $V$. En otras palabras, si se colorean los nodos $U$ de verde y los nodos $V$ de morado, unicamente existen enlaces que conecten nodos de diferentes colores.


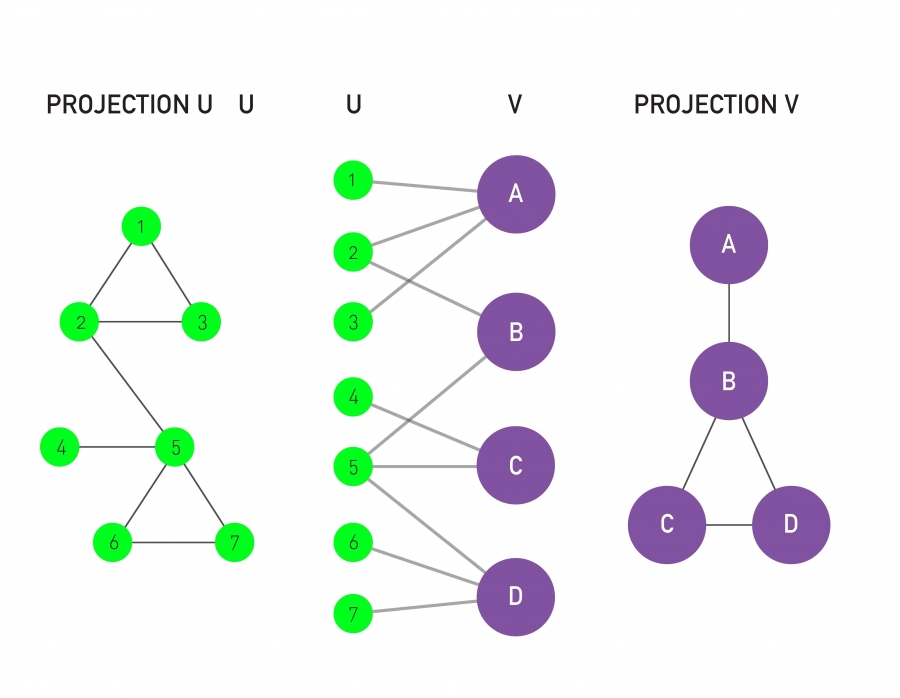
Ejemplo de grafo bipartito. Fuente: Network Science - Albert-László Barabási.


Es posible generar dos proyecciones para cada red bipartita. La primera proyección conecta nodos $U$ si estos están conectados con el mismo nodo $V$ en la representación bipartita. La segunda proyección conecta nodos $V$ si estos están conectados con el mismo nodo $U$ en la representación bipartita.

Volviendo al ejemplo anterior de una red bipartita, en la que un conjunto de nodos corresponde a las películas ($U$) y el otro a los actores ($V$), y cada película está conectada a los actores que actúan en ella; la primera proyección de esta red conecta los nodos de actores sí estos han actuado en la misma película. La otra proyección, conecta las películas que comparten al menos un actor en su reparto.

Caminos y distancias


La distancia física desempeña un papel clave en las interacciones entre los componentes de los sistemas. Por ejemplo, la distancia física entre dos ciudades influye al número de visitantes que viajan de una ciudad a otra.

En las redes, la distancia es un concepto diferente a la distancia física. Si se plantea la pregunta: ¿Cuál es la distancia entre dos usuarios de una red social? La distancia física deja de ser relevante porque dos individuos que viven en el mismo edificio pueden no conocerse y tener muy buenos amigos en otras partes del mundo.

En las redes, la distancia física se reemplaza por la longitud del camino. Un camino entre dos nodos es una ruta que se inicia en el primer nodo y recorre los enlaces de la red pasando por distintos nodos hasta llegar al segundo nodo. La longitud del camino representa el número de enlaces que contiene el camino entre dos nodos.

En la ciencia de las redes, los caminos desempeñan un papel central. A continuación, se describen algunas de sus propiedades más importantes:

Reciprocidad

En una red no dirigida, la distancia entre el nodo $i$ y el nodo $j$ es la misma que la distancia entre el nodo $j$ y el nodo $i$ ($d_{ij}$ = $d_{ji}$). Por lo contrario, en una red dirigida, a menudo $d_{ij}$ $\neq$ $d_{ji}$. Además, en una red dirigida, la existencia de un camino desde el nodo $i$ al nodo $j$ no garantiza la existencia de un camino desde $j$ a $i$.

Camino más corto entre dos nodos

En las redes determinar la distancia entre dos nodos equivale a identificar el camino más corto entre dichos nodos. La distancia (o camino más corto) $d_{ij}$ entre dos nodos $i$ y $j$ se puede calcular directamente a partir de la matriz de adyacencia $A_{i j}$. Basta con multiplicar la matriz de adyacencia por sí misma tantas veces como distancia entre dos nodos.

  • $d_{i j}=1$: Si hay un enlace directo entre $i$ y $j$, entonces $A_{i j}=1$ ( $A_{i j}=0$ de lo contrario $)$

  • $d_{i j}=2$: Si hay un camino de longitud 2 entre $i$ y $j$, entonces $A_{i k} A_{k j}=1\left(A_{i k} A_{k j}=0\right.$ de lo contrario). La cantidad de caminos $d_{i j}=2$ entre $i$ y $j$ es

$$ N_{i j}^{(2)}=\sum_{k=1}^N A_{i k} A_{j k}=A_{i j}^2 $$

​ La cantidad de caminos de longitud $d$ entre $i$ y $j$ es ​ $$ N_{i j}^{(d)}=A_{i j}^d $$

Estas ecuaciones son válidas tanto para redes dirigidas como no dirigidas.

En otras palabras, para obtener la distancia de orden 2 entre cualquier par de nodos, basta con multiplicar la matriz de adyacencia por sí misma. Si la multiplicamos por sí misma n veces, obtenemos la matriz de distancias de orden n.

Así, la matriz de distancia de orden 2 nos mostrará todos los pares de nodos que están conectados con un nodo intermedio. En el siguiente ejemplo, los nodos 2 y 5 tienen entre medias los nodos 4 y 1, es decir, existen dos caminos posibles de orden 2 que los conectan: el 2-4-5 y el 2-1-5. Por este motivo, si se multiplica la matriz de adyacencia por sí misma, se obtiene que el elemento [2,5] de la matriz de distancias es 2. Lo que quiere decir que existen dos caminos de distancia 2 entre los nodos 2 y 5.

Ejemplo de un grafo y su matriz de adyacencia. Al ser un grafo no dirigido, la matriz es simétrica.

Propiedades de redes y nodos

Las siguientes son algunas propiedades importantes de las redes y nodos en teoría de grafos. En artículos sucesivos se explicarán con más detalle, incluyendo su formulación e implicaciones matemáticas.

  • Grado de un nodo: el número de enlaces que tiene un nodo. Los grafos dirigidos presentan dos tipos de grado "in degree" para conexiones entrantes y "out degree" para conexiones salientes.
  • Vecindario de un nodo: los nodos a los que está conectado directamente un nodo.
  • Grado medio: el promedio del grado de todos los nodos en una red.
  • Densidad: el número de enlaces en una red dividido por el número máximo de enlaces posibles. La densidad proporciona una idea de qúan poblada de enlaces está la red.
  • Componentes conectadas: grupos de nodos conectados entre sí. No tienen porqué existir todas la conexiones, pero sí que desde cualquier nodo puedas viajar al resto de nodos.
  • Caminos y ciclos: un camino es una secuencia de enlaces que conectan dos nodos, mientras que un ciclo es un camino que comienza y termina en el mismo nodo.
  • Centralidad: medida de la importancia de un nodo en una red, según su grado, vecindario, caminos y ciclos, entre otros factores.
  • Clustering: medida de la cantidad de enlaces existentes entre los vecinos de un nodo.
  • Cliqué: conjunto de nodos todos conectados con todos.
  • Sub-grafo: la red resultante al seleccionar únicamente una serie de nodos.

Centralidad de los nodos


La centralidad es un concepto utilizado para medir la importancia de los nodos en un grafo. Las tres medidas de centralidad más importantes son:

  • Centralidad de grado: es la medida más simple, se basa en el número de enlaces que tiene un nodo, la suma de enlaces que entran y salen.
  • Centralidad de intermediación: mide la cantidad de caminos que pasan por un nodo.
  • Centralidad de cercanía: mide la distancia promedio desde un nodo a todos los demás nodos del grafo.

Para conocer más detalle de las propiedades de los grafos, puedes visitar el siguiente capítulo de la serie XX.

Grafos con NetworkX


NetworkX es una de las librerías de Python más utilizadas para trabajar con grafos y redes. NetworkX permite crear, manipular y analizar grafos de manera eficiente.

Una de las principales ventajas de NetworkX es su capacidad para trabajar con grafos de gran tamaño y complejidad, permitiendo manejar grafos con millones de nodos y enlaces. La librería cuenta con una gran variedad de funcionalidades que permiten crear, importar y exportar grafos en múltiples formatos, así como analizar las propiedades de estas redes (grado medio, la densidad, el coeficiente de clustering, el camino más corto entre dos nodos, y muchas otras más). Además, cuenta con una serie de algoritmos para buscar patrones, como la detección de comunidades, detección de centralidad y detección de componentes conectados. Todas estas propiedades se irán viendo en artículos sucesivos.

NetworkX también es compatible con otras librerías de Python, como NumPy, SciPy, Matplotlib o Pytorch, lo que permite integrar fácilmente el análisis de redes en un flujo de trabajo de análisis de datos más amplio.

Funciones importantes de NetworkX


A continuación, se muestra un listado con algunas de las funciones más utilizadas de NetworkX.

  • Creación de grafos: NetworkX permite crear grafos vacíos o con nodos y enlaces específicos utilizando funciones como Graph() (grafos no dirigidos), DiGraph() (grafos dirigidos), o incluso para conjuntos de grafos con MultiGraph() y MultiDiGraph().
  • Agregar nodos y enlaces: Se pueden agregar nodos y enlaces a un grafo existente de forma manual, bien uno a uno con add_node() y add_edge(), o desde una lista con add_nodes_from() y add_edges_from(). También pueden añadirse desde un archivo o DataFrame con from_pandas_edgelist(). Para grafos ponderados se utiliza la función add_weighted_edges_from.
  • Información del grafo: Se pueden obtener información básica del grafo, como el número de nodos y enlaces, utilizando las funciones number_of_nodes(), number_of_edges(). Utilizando nodes() y edges() se accede a la meta-información de nodos y ejes.
  • Vecinos y grado: Se pueden identificar los vecinos y el grado de un nodo utilizando las funciones: neighbors() y degree(); para redes dirigidas se utiliza in_degree() y out_degree().
  • Centralidad: Se pueden calcular medidas de centralidad, como la centralidad de grado, la centralidad de intermediación, y la centralidad entre los nodos utilizando las funciones degree_centrality(), betweenness_centrality() y closeness_centrality().
  • Componentes conectadas: Se pueden encontrar las componentes conectadas de un grafo utilizando la función connected_components().
  • Lectura y escritura de archivos: NetworkX permite leer y escribir grafos en varios formatos de archivo utilizando read_edgelist(), write_edgelist(), read_adjlist() y write_adjlist().
  • Algoritmos de optimización: NetworkX tiene integrados algoritmos de optimización como el camino más corto y el flujo máximo. Se accede a ellos con las funciones shortest_path() y dijkstra_path().
  • Subgrafos: Se pueden generar subgrafos de un grafo utilizando la función subgraph(), dando una lista de nodos como input.
  • Operaciones de conjunto: NetworkX permite realizar operaciones de conjunto en grafos tales como la unión, la intersección y la diferencia utilizando union(), intersection() y difference().
  • Matriz de adyacencia: Con la función nx.adjacency_matrix(G) se obtiene la matriz de adyacencia de un grafo. Por defecto, está en formato sparse, para verla por pantalla hay que utilizar la función to_dense() de numpy.
  • Gráfico de grafos:La función draw() permite dibujar grafos utilizando la ibrería Matplotlib.

Creación de grafos no dirigidos


NetworkX permite crear redes de manera manual, añadiendo los nodos y ejes uno por uno o desde un archivo o un DataFrame que contenga las conexiones. Esto último es especialmente útil cuando se trabaja con datos de redes que ya han sido recopilados y se encuentran en un formato estructurado.

Creación manual

In [1]:
# Librerías
# ======================================================================================
import networkx as nx
import pandas as pd
import warnings
import matplotlib.pyplot as plt

warnings.filterwarnings("ignore")

Para crear un grafo en NetworkX, se debe crear un objeto de tipo "Grafo" utilizando la función nx.Graph(). Esta función crea un grafo vacío, sin nodos ni ejes, al que se pueden agregar elementos más adelante.

In [2]:
# Creación de una instancia de tipo "Grafo"
# ======================================================================================
G = nx.Graph()
print(G)

Graph with 0 nodes and 0 edges

Se verifica que es un grafo no dirigido.

In [3]:
G.is_directed()
Out[3]:
False

Una vez que el objeto Grafo ha sido creado, se puede poblar con nodos y conexiones. Para ello se utilizan dos métodos:

  • add_node: añade un único nodo al grafo.
  • add_nodes_from: añade multiples nodos al grafo.
  • add_edge: añade un eje entre los nodos u y v. Si los nodos no existen, se crean y añaden automáticamente al grafo.
  • add_edges_from: mismo comportamiento que add_edge pero utilizando una colección de ejes. Cada eje se define con una tupla (u, v).

El nombre de los nodos puede ser tanto de numérico como caracteres.

In [4]:
# Añadir un único nodo
# ======================================================================================
fig, ax = plt.subplots(figsize=(1,1))
G.add_node("A")
nx.draw(G, with_labels=True, ax=ax)
print(G)

Graph with 1 nodes and 0 edges
In [5]:
# Añadir multiples nodos
# ======================================================================================
G.add_nodes_from(["B", "C"])

fig, ax = plt.subplots(figsize=(3, 2))
nx.draw(G, with_labels=True, ax=ax)
ax.set_xlim([1.2*x for x in ax.get_xlim()])
ax.set_ylim([1.2*y for y in ax.get_ylim()])
print(G)

Graph with 3 nodes and 0 edges
In [6]:
# Añadir un único eje
# ======================================================================================
G.add_edge("A", "B")

fig, ax = plt.subplots(figsize=(3, 2))
nx.draw(G, with_labels=True, ax=ax)
ax.set_xlim([1.2*x for x in ax.get_xlim()])
ax.set_ylim([1.2*y for y in ax.get_ylim()])
print(G)

Graph with 3 nodes and 1 edges
In [7]:
# Añadir múltiples ejes
# ======================================================================================
G.add_edges_from([("A", "C"), ("B", "C")])

fig, ax = plt.subplots(figsize=(3, 2))
nx.draw(G, with_labels=True, ax=ax)
ax.set_xlim([1.2*x for x in ax.get_xlim()])
ax.set_ylim([1.2*y for y in ax.get_ylim()])
print(G)

Graph with 3 nodes and 3 edges

Si se añade una conexión cuyos nodos no existen, se crean automáticamente.

In [8]:
G.add_edges_from([("D", "E"), ("E", "F")])

fig, ax = plt.subplots(figsize=(4, 4))
nx.draw(G, with_labels=True, ax=ax)
ax.set_xlim([1.2*x for x in ax.get_xlim()])
ax.set_ylim([1.2*y for y in ax.get_ylim()])
print(G)

Graph with 6 nodes and 5 edges

La matriz de adyacencia correspondiente es:

In [9]:
adjM = nx.adjacency_matrix(G)

# Se convierte la matriz de formato sparse a dense para poder imprimirla
adjM = adjM.todense()
adjM
Out[9]:
matrix([[0, 1, 1, 0, 0, 0],
        [1, 0, 1, 0, 0, 0],
        [1, 1, 0, 0, 0, 0],
        [0, 0, 0, 0, 1, 0],
        [0, 0, 0, 1, 0, 1],
        [0, 0, 0, 0, 1, 0]])

Y el número de nodos y ejes:

In [10]:
print(G.number_of_edges())
print(G.number_of_nodes())

5
6

La información de los nodos y ejes del grafo está almacenada en los attributos nodes y edges.

In [11]:
print(f"Nodos del grafo: {G.nodes}")
print(f"Ejes del grafo: {G.edges}")

Nodos del grafo: ['A', 'B', 'C', 'D', 'E', 'F']
Ejes del grafo: [('A', 'B'), ('A', 'C'), ('B', 'C'), ('D', 'E'), ('E', 'F')]

Creación desde un DataFrame

Para crear un grafo a partir de un dataframe de pandas, la información tiene que estar estructurada de tal forma que una columna represente el incio de cada eje y otra el destino. Por ejemplo, para representar que existen dos nodos ("A" y "B") conectados entre si, se necesita una fila que contenga el valor "A" en una columna y "B" en otra. Esta información es suficiente para que se creen los dos nodos y la conexión entre ambos.

In [12]:
# Dataframe con las conexiones del grafo
# ======================================================================================
conexiones = pd.DataFrame(
    {
        "inicio": ["A", "B", "C"],
        "fin": ["C", "C", "D"],
    }
)
conexiones
Out[12]:
inicio fin
0 A C
1 B C
2 C D

En la función from_pandas_edgelist se indica la columna de origen y destino (para grafos no dirigidos, se elige un origen indistintamente).

In [13]:
# Crear un grafo a partir de un Dataframe
# ======================================================================================
fig, ax = plt.subplots(figsize=(3,2))
G = nx.from_pandas_edgelist(conexiones, source="inicio", target="fin")
nx.draw(G, with_labels=True, ax=ax)

Creación de grafos dirigidos

Creación manual

Como se ha explicado anteriormente, los enlaces de los grafos dirigidos tienen una dirección definida (los enlaces de estos grafos se representan con una flecha). El proceso de creación de un grafo dirigido es esquivalente al de un grafos no dirigido pero utilizando DiGraph en luigar de Graph.

In [14]:
# Creación de un grafo dirigido".
# ======================================================================================
G = nx.DiGraph()

# Conexiones
G.add_edges_from([(1, 2), (2, 3), (1, 4), (1, 5), (4, 2), (5, 4)])

# Representación gráfica
fig, ax = plt.subplots(figsize=(3,2))
nx.draw(G, with_labels=True, ax=ax)

Se verifica que sí es un grafo dirigido.

In [15]:
G.is_directed()
Out[15]:
True

Creación desde un DataFrame

El proceso de creación de un grafo dirigido desde un DataFrame es equivalente al de los grafos no dirigidos mostrado en el apartado anterior, con la única diferencia de que se ha de indicar el argumento create_using = nx.DiGraph.

In [16]:
# Crear un grafo dirigido a partir de un Dataframe
# ======================================================================================
G = nx.from_pandas_edgelist(
    conexiones,
    source = "inicio",
    target = "fin",
    create_using = nx.DiGraph
)
fig, ax = plt.subplots(figsize=(3,2))
nx.draw(G, with_labels=True, ax=ax)

Al tratarse de un grafo dirigido, su matriz de adjacencia no es simétrica.

In [17]:
adjM = nx.adjacency_matrix(G)
adjM = adjM.todense()
adjM
Out[17]:
matrix([[0, 1, 0, 0],
        [0, 0, 0, 1],
        [0, 1, 0, 0],
        [0, 0, 0, 0]])

Distancia entre dos nodos


Para obtener la distancia de orden 2 entre cualquier par de nodos, basta con multiplicar la matriz de adyacencia por sí misma. Si la multiplicamos por sí misma n veces, obtenemos la matriz de distancias de orden n.

In [18]:
# Creación del grafo
G = nx.Graph()

# Se añadennodos a grafo
G.add_edges_from([(1, 2), (2, 3), (1, 4), (1, 5), (4, 2), (5, 4)])

# Representación gráfica
fig, ax = plt.subplots(figsize=(3,2))
nx.draw(G, with_labels=True, ax=ax)
In [19]:
# Matrix de adyacencia
adjM = nx.adjacency_matrix(G).todense()
adjM
Out[19]:
matrix([[0, 1, 0, 1, 1],
        [1, 0, 1, 1, 0],
        [0, 1, 0, 0, 0],
        [1, 1, 0, 0, 1],
        [1, 0, 0, 1, 0]])

La matriz de distancia de orden 2 muestra todos los pares de nodos que están conectados con un nodo intermedio. En el ejemplo, los nodos 2 y 5 tienen entre medias los nodos 4 y 1, es decir, existen dos caminos posibles de orden 2 que los conectan: el 2-4-5 y el 2-1-5. Por ese motivo, si se multiplica la matriz de adyacencia por sí misma, el elemento [2, 5] de la matriz de distancias tiene el valor 2. Lo que indica que existen dos caminos de distancia 2 entre los nodos 2 y 5.

In [20]:
# Multiplicación de la matriz por sí misma de forma matricial
distancias_orden_dos = adjM @ adjM
distancias_orden_dos
Out[20]:
matrix([[3, 1, 1, 2, 1],
        [1, 3, 0, 1, 2],
        [1, 0, 1, 1, 0],
        [2, 1, 1, 3, 1],
        [1, 2, 0, 1, 2]])
In [21]:
# Los indices en python empiezan en 0
print(f"Caminos de orden dos entre los nodos 2 y 5 = {distancias_orden_dos[1, 4]}")

Caminos de orden dos entre los nodos 2 y 5 = 2

También se puede calcular el camino más corto (shortest path) utilizando directamente la función nx.shortest_path.

In [22]:
nx.shortest_path(G, source=2, target=5)
Out[22]:
[2, 1, 5]

Grafo ponderado


En un grafo ponderado, los ejes del grafo tienen un peso asociado. En la representación gráfica de este tipo de redes, los ejes se suelen mostrar con una anchura distinta en función de su peso.

In [23]:
# Creacion del grafo
G = nx.Graph()

# Nodos y vonexiones
G.add_weighted_edges_from(
    [(1, 2, 0.5),
    (2, 3, 0.9),
    (1, 4, 0.1),
    (1, 5, 0.75),
    (4, 2, 0.01),
    (5, 4, 0.3)]
)
G.edges(data=True)
Out[23]:
EdgeDataView([(1, 2, {'weight': 0.5}), (1, 4, {'weight': 0.1}), (1, 5, {'weight': 0.75}), (2, 3, {'weight': 0.9}), (2, 4, {'weight': 0.01}), (4, 5, {'weight': 0.3})])
In [24]:
# Se verifica que es un grafo no dirigido y ponderado
G.is_directed()
Out[24]:
False
In [25]:
nx.is_weighted(G)
Out[25]:
True
In [26]:
# Se muestra el peso de cada eje, así como los nodos que conecta
[a for a in G.edges(data=True)]
Out[26]:
[(1, 2, {'weight': 0.5}),
 (1, 4, {'weight': 0.1}),
 (1, 5, {'weight': 0.75}),
 (2, 3, {'weight': 0.9}),
 (2, 4, {'weight': 0.01}),
 (4, 5, {'weight': 0.3})]

Para extraer los pesos, se itera sobre cada eje y se accede al tercer elemento de la tupla.

In [27]:
weights = [a[2]["weight"] for a in G.edges(data=True)]
weights
Out[27]:
[0.5, 0.1, 0.75, 0.9, 0.01, 0.3]

Para dibujar un grafo ponderado con NetworkX, es necesario dibujar por separado nodos y ejes. En primer lugar se utiliza un utilizando un graph layout que define la posición de los nodos. Una vez definida su posición se representan los nodos y los ejes. Para este ejemplo se utiliza el spring_layout, pero hay muchos más.

In [28]:
# Definir la posición de los nodos utilizando un layout
pos = nx.spring_layout(G)

# Representar nodos y ejes
fig, ax = plt.subplots(figsize=(3,2))
nx.draw_networkx_nodes(
    G,
    pos = pos,
    ax = ax
)
nx.draw_networkx_edges(
    G,
    pos = pos,
    edgelist = G.edges,
    width = weights,
    ax = ax
);

Otros tipos de layout

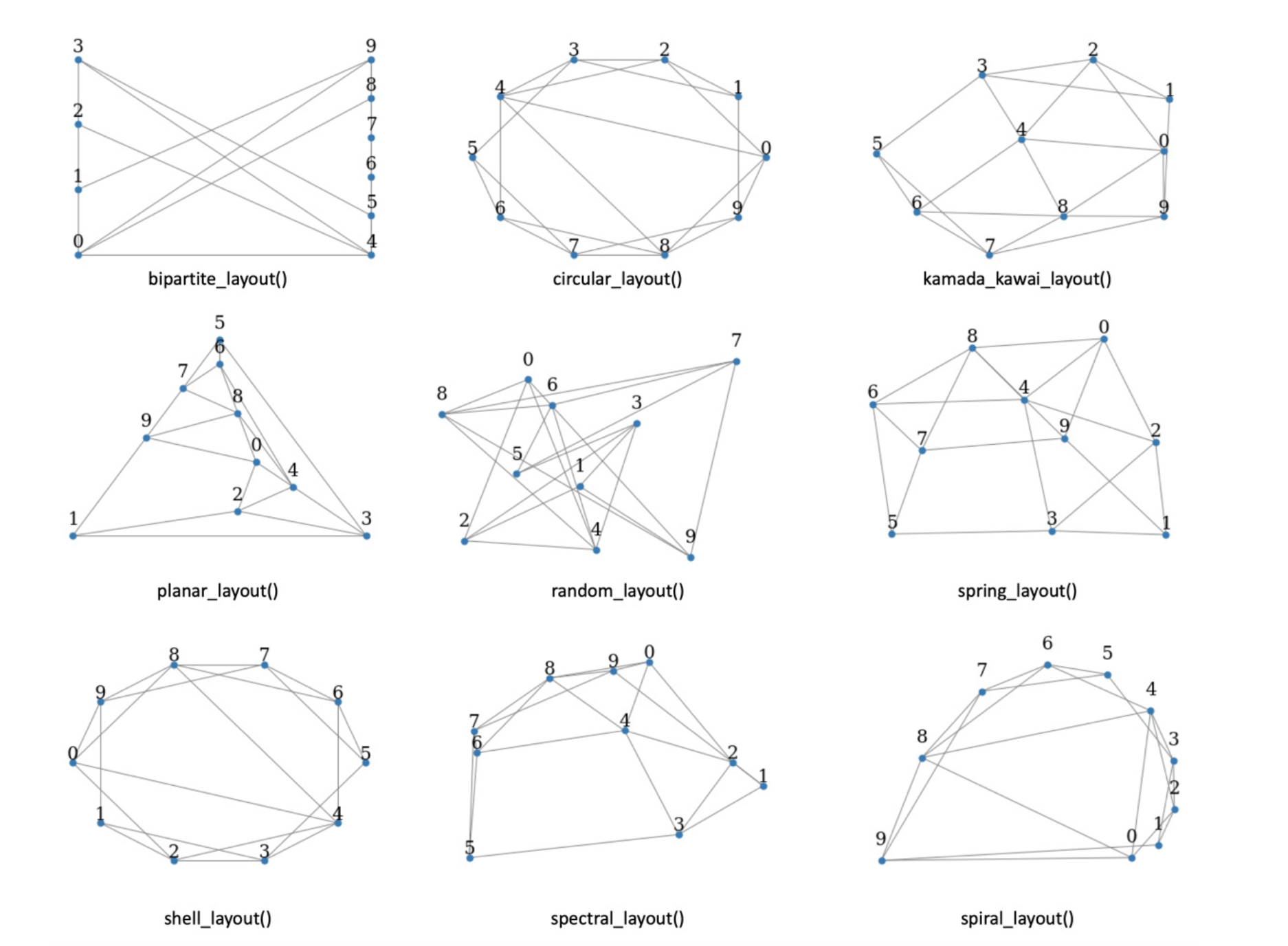
Ejemplos de los layouts más utilizados.

Representar de forma separada los nodos y ejes permite tener más control sobre las caracteristicas visuales, por ejemplo, el color de los nodos y ejes.

In [29]:
pos = nx.circular_layout(G)

fig, ax = plt.subplots(figsize=(3,3))
nx.draw_networkx_nodes(G, pos=pos, node_color="red", ax=ax)
nx.draw_networkx_edges(G, pos=pos, edgelist=G.edges, width=weights, edge_color="blue", ax=ax);

Grafo bipartito


Cuando los nodos de un grafo representan entidades de distinta naturaleza se utiliza el termino grafo bipartito. Un ejemplo común de este típo de grafos son las redes de publicaciones donde existen nodos de tipo "artículo" y otros de tipo "escritor".

En este tipo de grafos, las conexiones únicamente puden ocurrir entre nodos de distinta naturaleza, cada escritor está conectado a los artículos que ha escrito. No pueden existir conexiones directas entre artículos o entre escritores.

Para crear un grafo bipartito NetworkX se utiliza el método add_nodes_from() con el que se agregan los nodos indicando el tipo con el argumento bipartite y luego se utiliza el método add_edges_from() para agregar las relaciones entre ellos. A continuación, se muesra un ejemplo de cómo crear un grafo bipartito con dos conjuntos de nodos llamados "grupo A" y "grupo B".

In [30]:
# Crear un grafo bipartito vacío
G_peliculas_actores = nx.Graph()

# Agregar los nodos de cada grupo
G_peliculas_actores.add_nodes_from(["Pelicula_1", "Pelicula_2", "Pelicula_3"], bipartite="Peliculas")
G_peliculas_actores.add_nodes_from(["Actor_1", "Actor_2", "Actor_3"], bipartite="Actores")

# Agregar las relaciones entre los nodos
G_peliculas_actores.add_edges_from(
    [
        ("Pelicula_1", "Actor_1"),
        ("Pelicula_2", "Actor_2"),
        ("Pelicula_3", "Actor_3"),
        ("Pelicula_2", "Actor_3"),
        ("Pelicula_2", "Actor_1"),
    ]
)
In [31]:
G_peliculas_actores.nodes(data=True)
Out[31]:
NodeDataView({'Pelicula_1': {'bipartite': 'Peliculas'}, 'Pelicula_2': {'bipartite': 'Peliculas'}, 'Pelicula_3': {'bipartite': 'Peliculas'}, 'Actor_1': {'bipartite': 'Actores'}, 'Actor_2': {'bipartite': 'Actores'}, 'Actor_3': {'bipartite': 'Actores'}})

Para acceder al tipo de cada nodo se recorre cada nodo y se accede al attributo "bipartite".

In [32]:
tipo_nodo = [
    G_peliculas_actores.nodes[i]["bipartite"]
    for i in G_peliculas_actores.nodes()
]
tipo_nodo
Out[32]:
['Peliculas', 'Peliculas', 'Peliculas', 'Actores', 'Actores', 'Actores']
In [33]:
# colores para cada tipo de nodo en el grafo bipartito
colores = {"Peliculas": "red", "Actores": "blue"}
colores_nodos = [colores[n] for n in tipo_nodo]

fig, ax = plt.subplots(figsize=(5, 4))
nx.draw(
    G_peliculas_actores,
    pos=nx.spring_layout(G_peliculas_actores),
    with_labels=True,
    node_color=colores_nodos,
    ax=ax,
)

En el código anterior se utiliza la función spring_layout para posicionar los nodos en el gráfico. Con el arguemento with_labels=True se muestran las etiquetas de los nodos y con node_colorse asigna el color de cada nodo.

Una vez que creado el grafo bipartito, se puede hacer una proyección de éste para obtener un grafo no bipartito que contenga sólo los nodos de uno de los conjuntos. Para hacer esto, se emplea el método project() especificando el conjunto de nodos que se desea incluir en la proyección. A continuación se genera una proyección del grafo bipartito para obtener sólo los nodos del grupo 'Actores'.

In [35]:
# Se identifican los nodos del conjunto de interés
nodes_bipartite = [
    n[0]
    for n in G_peliculas_actores.nodes(data=True)
    if n[1]["bipartite"] == "Actores"
]

# Proyección del grafo bipartito para obtener sólo los nodos del grupo A
G_actores = nx.bipartite.projected_graph(G_peliculas_actores, nodes_bipartite)

fig, ax = plt.subplots(figsize=(4, 4))
nx.draw(G_actores, with_labels=True, ax=ax)
ax.set_xlim([1.2 * x for x in ax.get_xlim()])
ax.set_ylim([1.2 * y for y in ax.get_ylim()])
Out[35]:
(-1.4102627641846925, 1.0127652802293838)

Meta-información: atributos de nodos y ejes


En la matoria de los problemas de grafos reales, se dispone de información adicional de nodos y ejes. Los atributos de los nodos se añaden con el método networkx.set_node_atributes(Grafo, diccionario, nombre) y los atributos de los ejes se añaden con el método networkx.set_edge_atributes().

In [36]:
# Creación del grafo
G = nx.Graph()
G.add_edges_from([(1, 2), (2, 3), (1, 4), (1, 5), (4, 2), (5, 4)])
G.edges(data=True)
Out[36]:
EdgeDataView([(1, 2, {}), (1, 4, {}), (1, 5, {}), (2, 3, {}), (2, 4, {}), (4, 5, {})])
In [37]:
# Añadir atributos de los nodos
node_name = {1: "Jaime", 2: "María", 3: "Julio", 4: "Rosa", 5: "Alberto"}

node_aficiones = {
    1: ["Futbol"],
    2: ["Baile", "Pádel"],
    3: ["Golf", "Baile"],
    4: ["Cocina"],
    5: ["Cocina", "Jamón"],
}

nx.set_node_attributes(G, node_name, name="Nombre")
nx.set_node_attributes(G, node_aficiones, name="Aficiones")

# añadir atributos de los ejes
edges_weight = {
    (1, 2): 0.5,
    (2, 3): 0.9,
    (1, 4): 0.1,
    (1, 5): 0.75,
    (4, 2): 0.01,
    (5, 4): 0.3,
}

nx.set_edge_attributes(G, edges_weight, name="weight")

Para acceder a los atributos de nodos y ejes (meta-información) se utiliza G.nodes(data=True) o G.edges(data=True). Estos comandos devuelven una estructura en forma de diccionario donde la clave es el nombre del nodo y el valor contiene todos los atributos.

In [38]:
G.nodes(data=True)
Out[38]:
NodeDataView({1: {'Nombre': 'Jaime', 'Aficiones': ['Futbol']}, 2: {'Nombre': 'María', 'Aficiones': ['Baile', 'Pádel']}, 3: {'Nombre': 'Julio', 'Aficiones': ['Golf', 'Baile']}, 4: {'Nombre': 'Rosa', 'Aficiones': ['Cocina']}, 5: {'Nombre': 'Alberto', 'Aficiones': ['Cocina', 'Jamón']}})
In [39]:
G.edges(data=True)
Out[39]:
EdgeDataView([(1, 2, {'weight': 0.5}), (1, 4, {'weight': 0.1}), (1, 5, {'weight': 0.75}), (2, 3, {'weight': 0.9}), (2, 4, {'weight': 0.01}), (4, 5, {'weight': 0.3})])

Los atributos de ejes y nodos se pueden iterar directamente como si se tratase de un diccionario.

In [40]:
for m, n, w in G.edges(data=True):
    print(
        f"Eje que conecte el nodo {m} con el nodo {n} y tiene un peso de {w['weight']}."
    )

Eje que conecte el nodo 1 con el nodo 2 y tiene un peso de 0.5.
Eje que conecte el nodo 1 con el nodo 4 y tiene un peso de 0.1.
Eje que conecte el nodo 1 con el nodo 5 y tiene un peso de 0.75.
Eje que conecte el nodo 2 con el nodo 3 y tiene un peso de 0.9.
Eje que conecte el nodo 2 con el nodo 4 y tiene un peso de 0.01.
Eje que conecte el nodo 4 con el nodo 5 y tiene un peso de 0.3.

Caso de estudio: círculos sociales de Facebook (Stanford)


La base de datos "Social circles: Facebook" fue creada por investigadores de la universidad de Stanford en el año 2012. Este conjunto de datos consta de redes de amistad de Facebook. Los datos disponibles incluyen características de nodos (perfiles) y sus conexiones de amistad. Los datos fueron anonimizados reemplazando los nombres y otras identificaciones por un índice numérico. Pueden descargarse de la web de Stanford (https://snap.stanford.edu/data/ego-Facebook.html).

Libreías

In [41]:
# Librerías
# ==============================================================================
import pandas as pd
import warnings
import matplotlib.pyplot as plt
import networkx as nx
warnings.filterwarnings("ignore")

Lectura de los datos

In [42]:
# Lectura de datos
# ==============================================================================
facebook = pd.read_csv(
    "../data/facebook_combined.txt",
    header=None,
    sep=" ",
    names=["user_1", "user_2"],
)

Los datos consisten en una lista de ejes entre usuarios, cada fila es una relacción de amistad. Para reducir los requerimientos computacionales, en este ejemplo se emplean únicamente las 2000 primeras conexiones.

In [43]:
facebook = facebook[:2000]
facebook.head()
Out[43]:
user_1 user_2
0 0 1
1 0 2
2 0 3
3 0 4
4 0 5

Al ser relaciones de amistad y no tener direccionalidad, se representan mediante un grafo no direccional.

In [44]:
# Creación de grafo
# ==============================================================================
G_facebook = nx.from_pandas_edgelist(facebook, source="user_1", target="user_2", create_using=nx.Graph())

Información del grafo

Se muestra la información sobre la estructura del grafo.

In [45]:
print("Número de nodos:", G_facebook.number_of_nodes())
print("Número de enlaces:", G_facebook.number_of_edges())

Número de nodos: 713
Número de enlaces: 2000

Visualización de la red

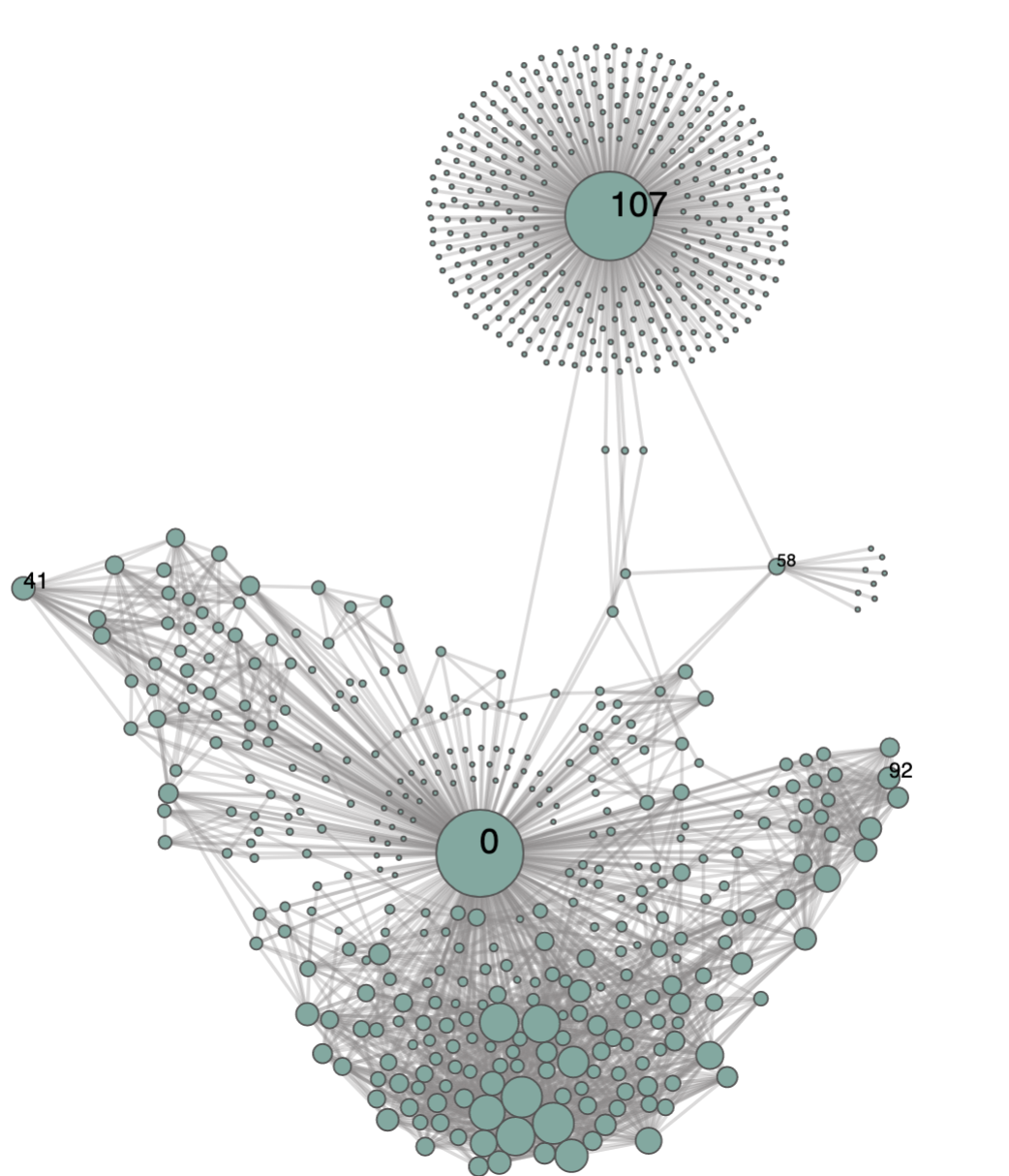
Al visualizar la red se observa que hay tres comunidades de usuarios:

  • Dos grandes conjuntos de usuarios altamente conectados.

  • Un grupo de unos pocos nodos centrales, algunos de los cuales conectan los otros dos grandes grupos.

In [46]:
fig, ax = plt.subplots(figsize=(9, 5))
spring_pos = nx.spring_layout(G_facebook)
nx.draw_networkx(
    G_facebook, pos=spring_pos, with_labels=False, node_size=15, ax=ax
)

Vecinos y grado

Para cualquier nodo del grafo, se puede conocer quienes son sus vecinos y su grado (el número de vecinos que tiene el nodo).

In [47]:
nodo_id = 4
vecinos = list(G_facebook.neighbors(nodo_id))
print("Vecinos del nodo {nodo_id}:", vecinos)

grado = G_facebook.degree[nodo_id]
print("Grado del nodo {nodo_id}:", grado)

Vecinos del nodo {nodo_id}: [0, 78, 152, 181, 195, 218, 273, 275, 306, 328]
Grado del nodo {nodo_id}: 10

Utilizando la función subgraph, se pueden extraer el nodo y sus vecinos, y analizaros con mayor detalle.

In [48]:
nodos = vecinos + [nodo_id]
G_s = nx.subgraph(G_facebook, nodos)

fig, ax = plt.subplots(figsize=(7, 4))
nx.draw_networkx(G_s, pos=spring_pos, with_labels=True, node_size=200, node_color='r', ax=ax)

Centralidad


Como se ha descrito anteriormente, la centralidad es un concepto utilizado para medir la importancia de los nodos en un grafo.

In [49]:
# Métricas de centralidad para un único nodo
# ==============================================================================
nodo_id = 4

# 1. **Centralidad de grado**
# Se basa en el número de enlaces que tiene un nodo. Es el número de enlaces que entran y salen de un nodo.
centralidad_grado = nx.degree_centrality(G_facebook)
print("Centralidad de grado:", centralidad_grado[nodo_id])

# 2. **Centralidad de intermediación**
# Mide la cantidad de caminos que pasan por un nodo.
centralidad_intermediacion = nx.betweenness_centrality(G_facebook)
print("Centralidad de intermediación:", centralidad_intermediacion[nodo_id])

# 3. **Centralidad de cercanía**
# Mide la distancia promedio desde un nodo a todos los demás nodos del grafo.
centralidad_cercania = nx.closeness_centrality(G_facebook)
print("Centralidad de cercanía:", centralidad_cercania[nodo_id])

Centralidad de grado: 0.014044943820224719
Centralidad de intermediación: 4.345833530871221e-05
Centralidad de cercanía: 0.40022484541877457
In [50]:
# Métricas de centralidad para todos los nodos
# ==============================================================================
grado = pd.DataFrame.from_dict(centralidad_grado, orient='index',columns=["grado"])
intermendiacion = pd.DataFrame.from_dict(centralidad_intermediacion, orient='index',columns=["intermediacion"])
cercania = pd.DataFrame.from_dict(centralidad_cercania, orient='index',columns=["cercania"])
centralidad = pd.concat([grado, intermendiacion, cercania], axis=1)
centralidad
Out[50]:
grado intermediacion cercania
0 0.487360 0.704019 0.661096
1 0.023876 0.000119 0.401806
2 0.014045 0.000026 0.400225
3 0.023876 0.000079 0.401806
4 0.014045 0.000043 0.400225
... ... ... ...
1222 0.001404 0.000000 0.401127
1223 0.001404 0.000000 0.401127
1224 0.001404 0.000000 0.401127
1225 0.001404 0.000000 0.401127
1226 0.001404 0.000000 0.401127

713 rows × 3 columns

Se puede observar que, por norma general, los nodos con alta centralidad de grado, también tienen alta centralidad de intermediación. Sin embargo, se pueden encontar algunos nodos que tienen alta intermeciación pero bajo grado.

En este grafo, se pueden observar cuatro nodos con alta intermediación y bajo grado. Estos cuatro nodos son los cuatro nodos que estaban entre los dos grandes grupos de usuarios.

In [51]:
fig, ax = plt.subplots(figsize=(6, 3))
centralidad.plot.scatter(x="grado", y="intermediacion", ax=ax)
ax.set_xscale('log')
ax.set_yscale('log')

Visualización avanzada de redes


Existen otras librerías con las que se pueden visualizar redes mucho más grandes de forma muy eficiente e interactiva. En próximos artículos se mostrarán con detalle las principales alternativas.

Representación generada con Netwulf.

Información de sesión

In [ ]:
import session_info
session_info.show(html=False)

-----
matplotlib          3.6.3
networkx            3.0
netwulf             0.1.5
pandas              1.5.3
session_info        1.0.0
-----
IPython             8.9.0
jupyter_client      8.0.2
jupyter_core        5.2.0
notebook            6.2.0
-----
Python 3.9.16 (main, Jan 11 2023, 16:05:54) [GCC 11.2.0]
Linux-5.15.0-1028-aws-x86_64-with-glibc2.31
-----
Session information updated at 2023-02-11 16:42

Bibliografía


Network Science - Albert-László Barabási

https://towardsdatascience.com/graph-machine-learning-with-python-pt-1-basics-metrics-and-algorithms-cc40972de113

https://towardsdatascience.com/graph-machine-learning-with-python-pt-2-random-graphs-and-diffusion-models-of-cryptopunks-trading-99cd5170b5ea

https://towardsdatascience.com/graph-machine-learning-with-python-part-3-unsupervised-learning-aa2854fe0ff2

https://ericmjl.github.io/Network-Analysis-Made-Simple/01-introduction/03-viz/

http://networksciencebook.com/

¿Cómo citar este documento?

Introducción a grafos y redes con Python por Fernando Carazo y Joaquín Amat, available under a Attribution 4.0 International (CC BY 4.0) at https://www.cienciadedatos.net/documentos/pygml01-introduccion-grafos-redes-python.html DOI


¿Te ha gustado el artículo? Tu ayuda es importante

Mantener un sitio web tiene unos costes elevados, tu contribución me ayudará a seguir generando contenido divulgativo gratuito. ¡Muchísimas gracias! 😊


Creative Commons Licence
Este contenido, creado por Fernando Carazo y Joaquín Amat Rodrigo, tiene licencia Attribution-NonCommercial-ShareAlike 4.0 International.