Detección de comunidades en grafos y redes con python
Más sobre ciencia de datos: cienciadedatos.net
Introducción¶
La detección de comunidades, también conocida como partición de grafos, hace referencia al conjunto de técnicas no supervisadas utilizadas para encontrar grupos de nodos altamente interconectados. Más concretamente, la detección de comunidades trata de identificar subconjuntos de nodos que están muy conectados entre ellos y, al mismo tiempo, poco conectados con el resto de nodos de la red.
La detección de comunidades tiene multitud de aplicaciones, tales como la identificación de grupos de personas con intereses similares, la clasificación de proteínas con funciones relacionadas y la agrupación de sitios web con temas comunes.
Son muchos los métodos de detección de comunidades que se han desarollado, parte de ellos como adaptaciones de algoritmos de clustering, con la principal diferencia de que la similitud entre nodos se cuantifica utilizando únicamente la topología de la red.
En este documento, se hace énfasis en el algoritmo de Louvain, uno de los algoritmos más utilizados debido a su eficiencia y escalabilidad. Para aquellos que no estén familiarizados con el análisis de grafos, se recomienda leer introducción a grafos y redes con Python.

Detección de comunidades¶
En términos simples, una comunidad es un grupo de nodos que tienen una alta densidad de conexiones entre ellos, pero una baja densidad de conexiones con nodos fuera del grupo. La detección de comunidades trata de encontrar esos conjuntos de nodos que están más conectados entre sí que con el resto del grafo. Existen multitud de algoritmos para detectar comunidades, y el algoritmo adecuado depende del tipo de grafo y del problema en cuestión. Algunos de los algoritmos más utilizados son:
Algoritmo de Girvan-Newman: este algoritmo se basa en la idea de eliminar progresivamente los enlaces que conectan los grupos de nodos con mayor densidad (enlaces con mayor betweenness centrality) hasta que queden subgrafos desconectados que representan las comunidades.
Algoritmo de Infomap: este algoritmo se basa en la idea de que los nodos de una comunidad tienen una probabilidad más alta de ser visitados por un recorrido aleatorio que los nodos del resto del grafo.
Algoritmo de Louvain: este algoritmo se basa en la idea de optimizar la métrica de modularidad, que busca maximizar el número de enlaces dentro de una comunidad y minimizar el número de enlaces entre comunidades. El concepto de la modularidad se explicará en detalle más adelante.
El algoritmo de Louvain es uno de los algoritmos más populares y eficientes para detectar comunidades en un grafo. Es la opción recomendable en situaciones en las que se desea encontrar comunidades en grandes redes. Las comunidades resultantes tienden a ser compactas y bien definidas.
Algoritmo de Louvain¶
Modularidad¶
El algoritmo de Louvain tiene como objetivo optimizar un concepto matemático denominado modularidad, una medida que se utiliza en la teoría de grafos para evaluar la calidad de una partición.
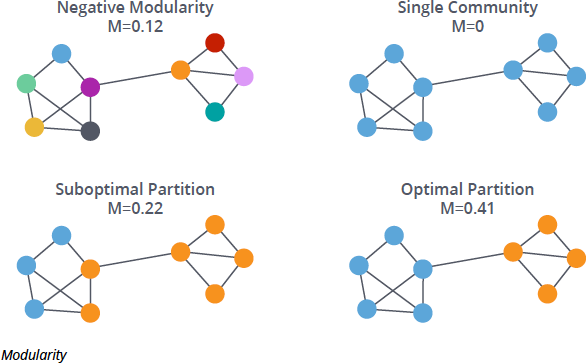
La modularidad se define como la diferencia entre el número de enlaces observado dentro de las comunidades y el número de enlaces esperados por azar. Una alta modularidad indica que las comunidades encontradas tienen más conexiones que las esperadas por azar y, por tanto, son compactas y bien definidas.
La modularidad tiene un rango de valores entre -0.5 y 1 y se define mediante la siguiente fórmula:
$$ M=\frac{1}{2 m} \sum_{i j}\left[A_{i j}-\frac{k_i k_j}{2 m}\right] \delta\left(c_i, c_j\right) $$dónde
$A_{i j}$ matriz de adyacencia (nodos $i$ y $j$). Puede ser de un grafo ponderado.
$k_i$ y $k_j$ son la suma de los pesos de la matriz de adyacencia de los ejes que conectan a los nodos $i$ y $j$. Si el grafo es no ponderado, equivale al grado del nodo, es decir, el número de conexiones.
$m$ es la suma de todos los pesos de la matriz de adyacencia. En un grafo no ponderado, es igual al número de ejes ($L$).
$c_i$ y $c_j$ son las comunidades a las que pertenecen los nodos $i$ y $j$.
$\delta$ es la función delta de Kronecker. Tiene valor $1$ si los nodos $i$ y $j$ pertenecen a la misma comunidad y $0$ en caso contrario. Por lo tanto, la fórmula sólo aplica si los nodos pertenecen a la misma comunidad.
Para un grafo no ponderado, la modularidad se puede simplificar a la siguiente fórmula:
$$ M=\frac{1}{2 L} \sum_{i j}\left[A_{i j}-\frac{k_i k_j}{2 L}\right] \delta\left(c_i, c_j\right) $$dónde $L$ es el número total de enlaces del grafo.
Una forma sencilla de entender la ecuación es la siguiente:
Para encontrar las comunidades de mayor calidad, se quiere maximizar la modularidad.
La fórmula únicamente toma valores distintos de cero cuando los nodos pertenecen a la misma comunidad, de lo contrario el delta de Kroneker vale 0.
Maximizar la ecuación implica que el primer término debe ser lo más alto posible, mientras que el segundo término debe ser lo más bajo posible.
$\sum_{i j}A_{i j}$ es el número de enlaces existentes dentro de una comunidad.
El segundo término de la ecuación representa el número de enlaces esperados por azar entre dos nodos. El número de enlaces posibles entre dos nodos es proporcional al producto de sus grados. Por ejemplo, si el grado de alguno de los nodos es 0, el número de enlaces esperados por azar es 0 (ya que uno de los nodos no tiene enlaces). El producto de los grados se divide por el número total de enlaces ($2L$) para convertirlo en una proporción.
Si el número de enlaces de la comunidad es mayor que el esperado por azar, el valor de la modularidad es positivo. Cuanto mayor sea la diferencia entre el número de enlaces dentro de la comunidad y el número de enlaces esperados por azar, mayor la modularidad.
En la siguiente imagen se muestran varios ejemplos de modularidad con distintas particiones. Se puede observar que la mejor partición es la de modularidad más alta.
Algoritmo¶
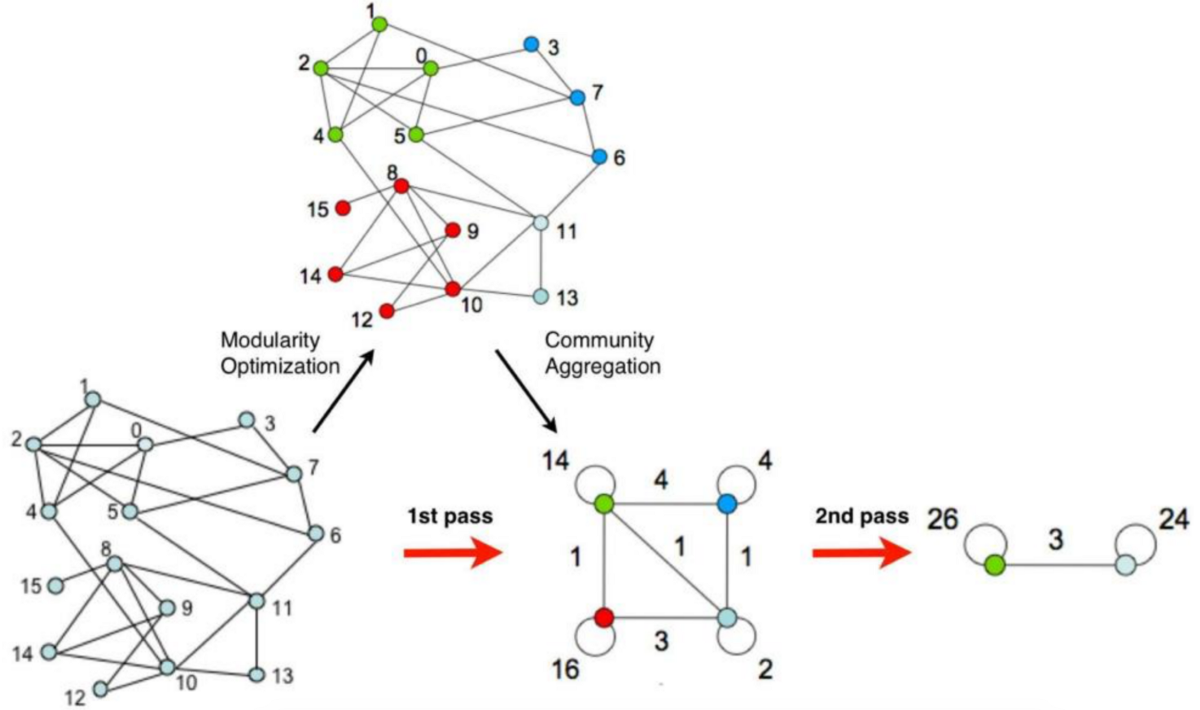
El algoritmo de Louvain es uno de los algoritmos más populares y eficientes para detectar comunidades en grafos. Se basa en la idea de maximizar el número de enlaces dentro de una comunidad y minimizar el número de enlaces entre comunidades (optimización de modularidad). Su funcionamiento se divide en dos fases: una fase de agrupamiento y una fase de refinamiento.
Fase de agrupamiento
En la fase de agrupamiento, cada nodo se asigna a su propia comunidad. Luego, se itera sobre cada nodo del grafo y se calcula la ganancia en modularidad que se obtendría al mover el nodo a una comunidad diferente. Si se obtiene una ganancia positiva, se mueve el nodo a la comunidad correspondiente. Esto se repite hasta que ya no se pueden obtener ganancias adicionales.
Fase de refinamiento
La segunda fase consiste en construir una nueva red cuyos nodos son las comunidades encontradas en la primera fase. Los pesos de los enlaces entre los nuevos nodos se calculan sumando del peso de los enlaces entre los nodos de las dos comunidades correspondientes. Al final de esta fase, se obtiene una partición del grafo con comunidades más compactas y mejor definidas que las obtenidas en la fase de agrupamiento.
Las dos fases anteriores se ejecutan hasta que no se obtiene ninguna ganancia de modularidad (o es inferior a un umbral). El resultado final es una partición del grafo en comunidades.
El algoritmo de Louvain fue propuesto por primera vez en un artículo titulado "Fast unfolding of communities in large networks" ("Despliegue rápido de comunidades en grandes redes"), publicado en la revista "Journal of Statistical Mechanics: Theory and Experiment" en 2008.
Control del tamaño de las comunidades: Resolución¶
El algoritmo de Louvain tiene un parámetro llamado resolution (resolución) que controla el grado de resolución de las comunidades detectadas. Un valor de resolución alto produce comunidades más pequeñas y específicas, mientras que un valor bajo produce comunidades más grandes y generales. Este es un parámetro importante que debe ser ajustado para cada caso.
La siguiente figura del artículo "Laplacian Dynamics and Multiscale Modular Structure in Networks" se muestra la influencia del parámetro resolution en la calidad de las particiones ($R(t)$). En la imagen, el parámetro time representa resolution. Se puede apreciar que, cuanto mayor es la resolución, más pequeñas son las comunidades encontradas.
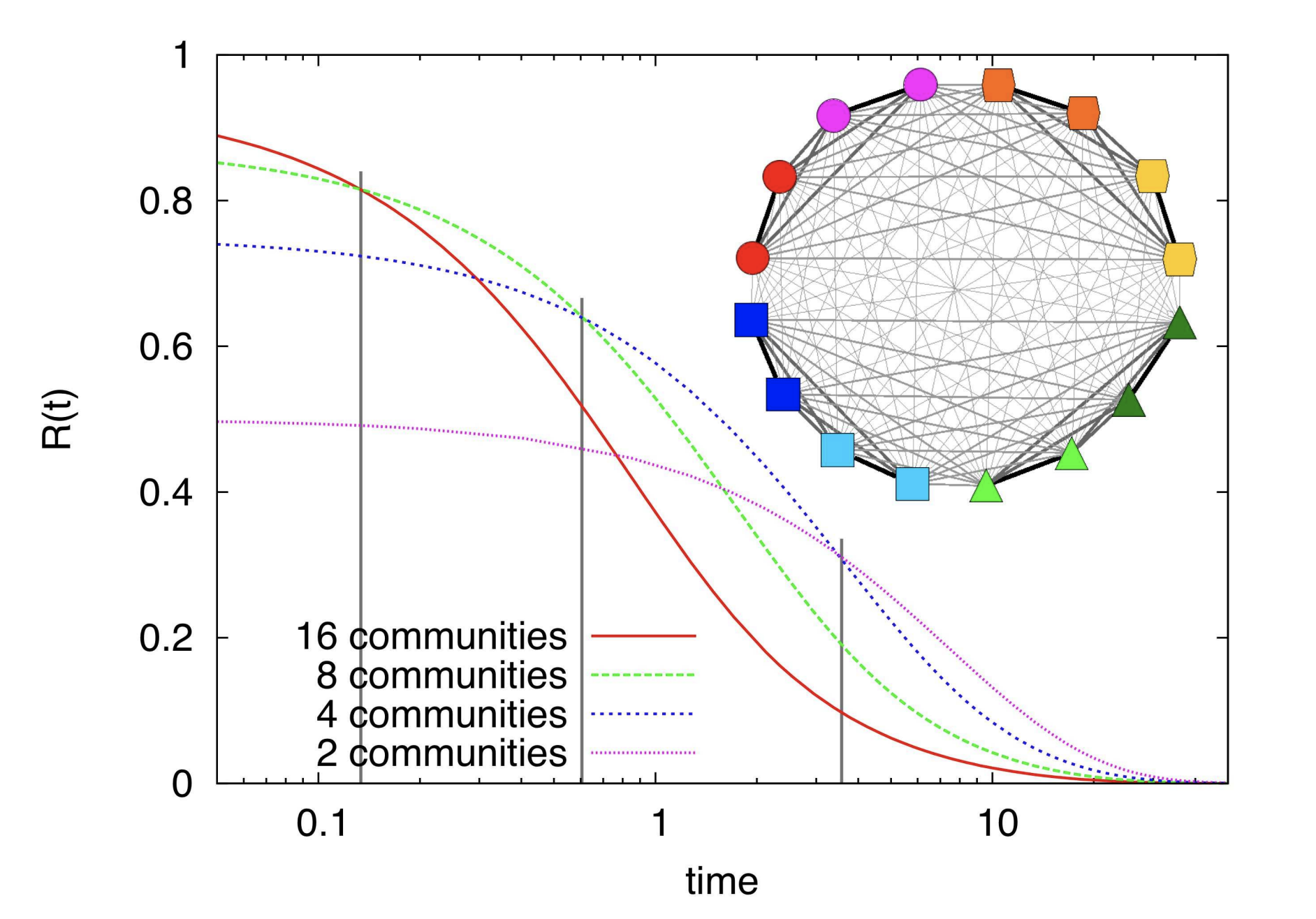
Es importante tener en cuenta que el valor de resolución óptimo depende de cada caso y del tamaño de las comunidades que se desean detectar. Por lo tanto, se recomienda experimentar con diferentes valores de resolución para encontrar la configuración que mejor se adapte a los objetivos de la detección de comunidades en un grafo determinado.
En primer lugar, se simula un grafo con la función barbell_graph de NetworkX. Se trata de un grafo con dos grupos de nodos conectados por una serie de nodos que actúan como enlace.
# Creación del grafo
# ======================================================================================
import networkx as nx
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(6, 4))
G = nx.barbell_graph(m1=10, m2=3)
nx.draw_networkx(G=G, ax=ax)
Los algoritmos de detección de comunidades implementados en networkx no se importan directamente al cargar la librería, para acceder a ellos es es necesario importar el módulo networkx.algorithms.community y luego utilizar la función con el algoritmo de interés, en este caso louvain_communities.
Esta función recibe como argumento un grafo de red y devuelve una lista de sets, donde cada set contiene los nodos de las comunidades detectadas. También están disponibles algunos parámetros opcionales que permiten configurar el algoritmo:
El parámetro
weightpermite especificar un atributo de peso en las conexiones del grafo.El parámetro
seedpermite especificar una semilla para la aleatorización.El parámetro
resolutionpermite ajustar el grado de resolución de las comunidades.El parámetro
thresholddiferencia mínima de modularidad entre dos iteraciones del algoritmo para considerar que hay una mejora.
# Detección de comunidades con Louvain
# ======================================================================================
import networkx.algorithms.community as nx_comm
comunidades = nx_comm.louvain_communities(
G = G,
weight = 'weight',
resolution = 1
)
comunidades
Los resultados muestran que se han detectado un total de tres comunidades.
# Tamaño de las comunidades
# ======================================================================================
[len(comunidad) for comunidad in comunidades]
Suele ser más util almacenar los resultados en forma de diccionario donde, cada nodo tiene asociado el identificador de la comunidad a la que pertenece.
comunidades_map = {}
for i in range(len(comunidades)):
comunidades_map.update(dict.fromkeys(comunidades[i], i))
comunidades_map
Filmente, se visualizan las comunidadmes encontradas coloreando cada nodo con el color de la comunidad a la que pertenece.
# Colorear los nodos en función de la comunidad
# ======================================================================================
import matplotlib.colors as mcolors
color_pallet = list(mcolors.TABLEAU_COLORS.values())
color_nodos = []
for node in G:
color_nodos.append(color_pallet[comunidades_map[node]])
fig, ax = plt.subplots(figsize=(6, 4))
nx.draw(G, node_color=color_nodos, with_labels=True, ax=ax)
plt.show()
Caso de estudio: círculos sociales de Facebook (Stanford)¶
Librerías¶
# Librerías
# ==============================================================================
import pandas as pd
import warnings
import matplotlib.pyplot as plt
import matplotlib.colors as mcolors
import networkx as nx
import networkx.algorithms.community as nx_comm
warnings.filterwarnings("ignore")
Datos¶
La base de datos "Social circles: Facebook" fue creada por investigadores de la universidad de Stanford en el año 2012. Este conjunto de datos representa redes de amistad de Facebook. Los datos disponibles incluyen características de nodos (perfiles) y sus conexiones de amistad. Los datos fueron anonimizados reemplazando los nombres y otras identificaciones por un índice numérico. Pueden descargarse de la web de Stanford (https://snap.stanford.edu/data/ego-Facebook.html).
# Lectura de datos
# ==============================================================================
facebook = pd.read_csv(
"https://raw.githubusercontent.com/JoaquinAmatRodrigo/Estadistica-machine-learning-python/master/data/facebook_combined.txt",
header = None,
sep = " ",
names = ["user_1", "user_2"],
)
Los datos consisten en una lista de ejes entre usuarios, cada fila es una relacción de amistad. Para reducir los requerimientos computacionales, en este ejemplo se emplean únicamente las 2000 primeras conexiones.
facebook = facebook[:5000]
facebook.head()
Creación del grafo¶
Al ser relaciones de amistad y no tener direccionalidad, se representan mediante un grafo no direccional.
# Creación del grafo
# ==============================================================================
G_facebook = nx.from_pandas_edgelist(
df = facebook,
source = "user_1",
target = "user_2",
create_using = nx.Graph()
)
Se muestra la información sobre la estructura del grafo.
print("Número de nodos:", G_facebook.number_of_nodes())
print("Número de enlaces:", G_facebook.number_of_edges())
Visualización de la red¶
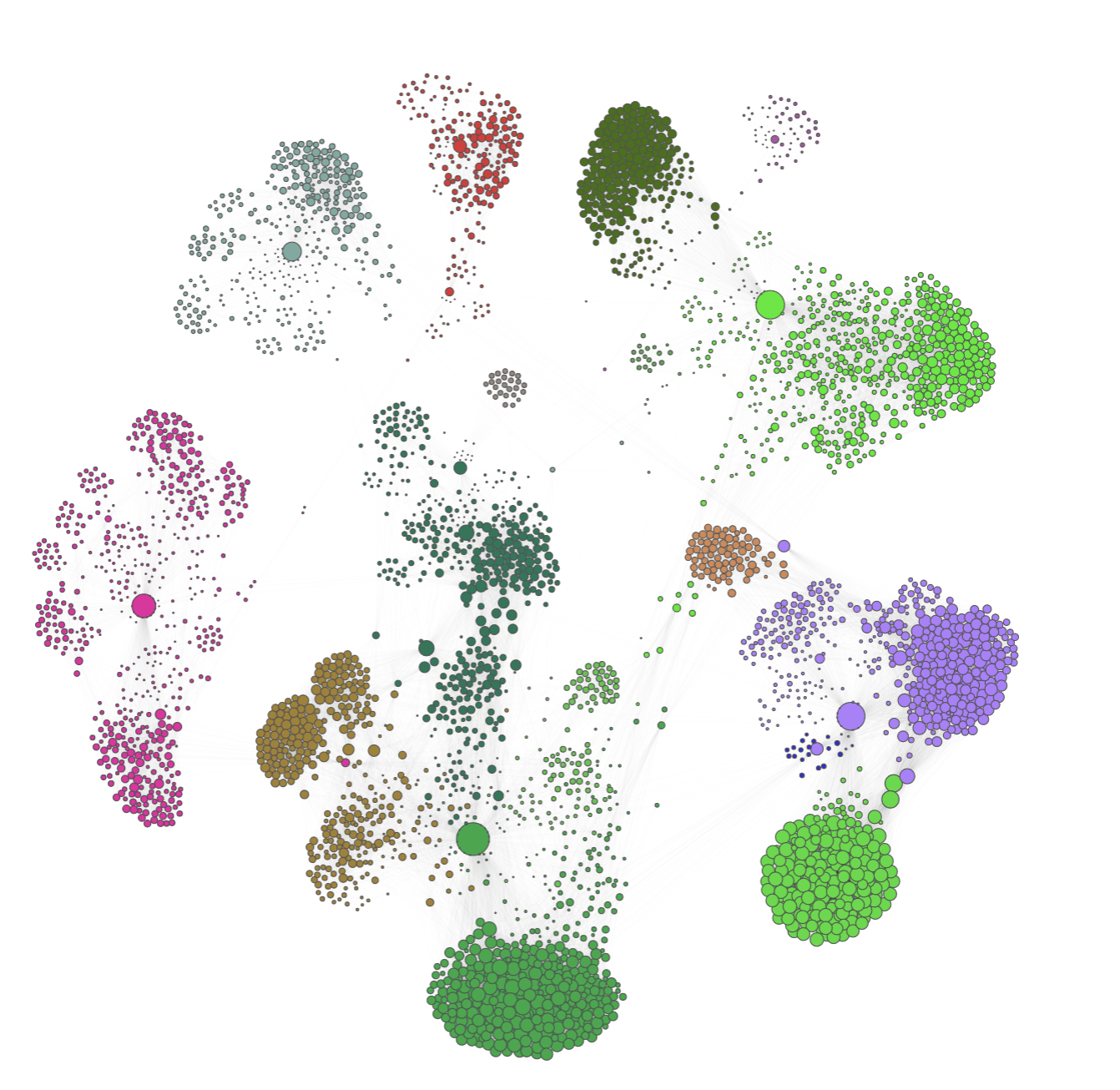
Al visualizar la red se observa que hay tres comunidades de usuarios:
Dos grandes conjuntos de usuarios altamente conectados.
Un grupo de unos pocos nodos centrales, algunos de los cuales conectan los otros dos grandes grupos.
fig, ax = plt.subplots(figsize=(9, 5))
spring_pos = nx.spring_layout(G_facebook)
nx.draw_networkx(
G = G_facebook,
pos = spring_pos,
with_labels = False,
node_size = 15,
ax = ax
)
Detección de comunidades¶
# Deteción de comunidades con Louvain
# ======================================================================================
comunidades = nx_comm.louvain_communities(
G = G_facebook,
weight = 'weight',
resolution = 0.2
)
print(f"Número de comunidades detectadas: {len(comunidades)}")
print(f"Tamaño de las comunidades detectadas: {[len(comunidad) for comunidad in comunidades]}")
Representación de la red y sus comunidades¶
Para visualizar las comunidades detectadas, se puede utilizar la función draw_networkx() de NetworkX. Esta función permite especificar un diccionario de colores para los nodos en función de su comunidad.
# Colorear los nodos en función de la comunidad
# ======================================================================================
color_pallet = list(mcolors.TABLEAU_COLORS.values())
comunidades_map = {}
for i in range(len(comunidades)):
comunidades_map.update(dict.fromkeys(comunidades[i], i))
comunidades_map
color_nodos = []
for node in G_facebook:
color_nodos.append(color_pallet[comunidades_map[node]])
fig, ax = plt.subplots(figsize=(9, 5))
spring_pos = nx.spring_layout(G_facebook)
nx.draw_networkx(
G = G_facebook,
pos = spring_pos,
with_labels = False,
node_size = 15,
node_color = color_nodos,
ax = ax
)
Cabe destacar que, para representar gráficamente los grafos, existen librerías mucho más potentes que las utilizadas en este documento. Por ejemplo, la librería netwulf permite dibujar grafos de una forma mucho más eficiente y con un mayor control sobre el aspecto de los nodos y las aristas, así como de la posición de los nodos en el espacio.
Conclusiones¶
En este documento se ha descrito cómo detectar comunidades en redes sociales utilizando el algoritmo de Louvain. Este algoritmo es una de las técnicas más populares para la detección de comunidades en redes sociales. Sin embargo, existen otras técnicas que pueden ser útiles en algunos casos. Por ejemplo, el algoritmo de Girvan-Newman, que permite detectar comunidades en redes dirigidas.
Información de sesión¶
import session_info
session_info.show(html=False)
Bibliografía¶
Network Science - Albert-László Barabási
V. D. Blondel, J.-L. Guillaume, R. Lambiotte and E. Lefebvre, "Fast unfolding of communities in large networks," J. Stat. Mech. (2008) P10008, p. 12, 2008.
"Laplacian Dynamics and Multiscale Modular Structure in Networks", R. Lambiotte, J.-C. Delvenne, M. Barahona
¿Cómo citar este documento?
Detección de comunidades en grafos y redes con python by Fernando Carazo and Joaquín Amat Rodrigo, available under a CC BY-NC-SA 4.0 at https://www.cienciadedatos.net/documentos/pygml01-introduccion-grafos-redes-python.html
¿Te ha gustado el artículo? Tu ayuda es importante
Mantener un sitio web tiene unos costes elevados, tu contribución me ayudará a seguir generando contenido divulgativo gratuito. ¡Muchísimas gracias! 😊
Este contenido, creado por Fernando Carazo y Joaquín Amat Rodrigo, tiene licencia Attribution-NonCommercial-ShareAlike 4.0 International.
Se permite:
-
Compartir: copiar y redistribuir el material en cualquier medio o formato.
-
Adaptar: remezclar, transformar y crear a partir del material.
Bajo los siguientes términos:
-
Atribución: Debes otorgar el crédito adecuado, proporcionar un enlace a la licencia e indicar si se realizaron cambios. Puedes hacerlo de cualquier manera razonable, pero no de una forma que sugiera que el licenciante te respalda o respalda tu uso.
-
NoComercial: No puedes utilizar el material para fines comerciales.
-
CompartirIgual: Si remezclas, transformas o creas a partir del material, debes distribuir tus contribuciones bajo la misma licencia que el original.
%%html