Más sobre ciencia de datos: cienciadedatos.net
- Regresión lineal con Python
- Regularización Ridge, Lasso y Elastic Net con Python
- Machine learning con Python y Scikit-learn
- Random Forest con Python
- Gradient Boosting con Python
Introducción¶
El análisis de componentes principales (Principal Component Analysis PCA) es un método de reducción de dimensionalidad que permite simplificar la complejidad de espacios con múltiples dimensiones a la vez que conserva su información.
Supóngase que existe una muestra con $n$ individuos cada uno con $p$ variables ($X_1$, $X_2$, ..., $X_p$), es decir, el espacio muestral tiene $p$ dimensiones. PCA permite encontrar un número de factores subyacentes $(z < p)$ que explican aproximadamente lo mismo que las $p$ variables originales. Donde antes se necesitaban $p$ valores para caracterizar a cada individuo, ahora bastan $z$ valores. Cada una de estas $z$ nuevas variables recibe el nombre de componente principal.
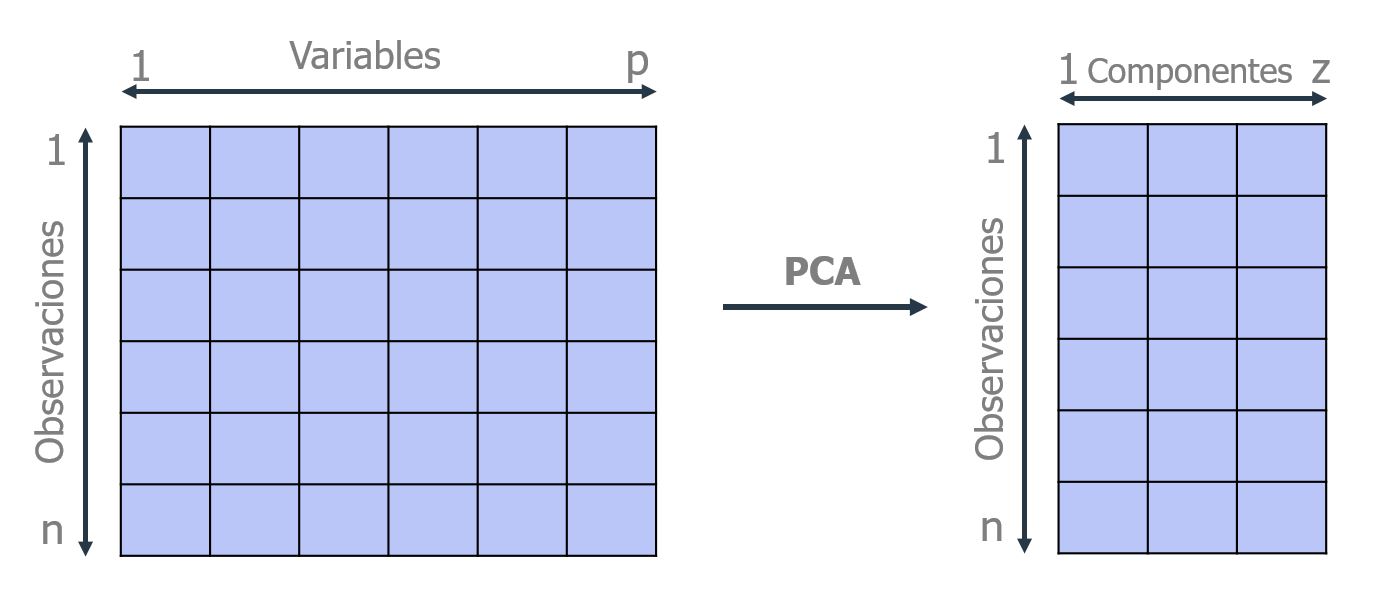
El método de PCA permite por lo tanto "condensar" la información aportada por múltiples variables en solo unas pocas componentes. Aun así, no hay que olvidar que sigue siendo necesario disponer del valor de las variables originales para calcular las componentes. Dos de las principales aplicaciones del PCA son la visualización y el preprocesado de predictores previo ajuste de modelos supervisados.
La librería scikitlearn contiene la clase sklearn.decomposition.PCA que implementa la mayoría de las funcionalidades necesarias para crear y utilizar modelos PCA. Para visualizaciones, Yellowbrick ofrece funcionalidades extra.
Álgebra lineal¶
En esta sección se describen dos de los conceptos matemáticos que se aplican en el PCA: eigenvectors y eigenvalues. Se trata simplemente de una descripción intuitiva con la única finalidad de facilitar el entendimiento del cálculo de componentes principales.
Eigenvectors¶
Los eigenvectors son un caso particular de multiplicación entre una matriz y un vector. Obsérvese la siguiente multiplicación:
$$\begin{pmatrix} 2 & 3 \\ 2 & 1 \end{pmatrix} x \begin{pmatrix} 3 \\ 2 \end{pmatrix} = \begin{pmatrix} 12 \\ 8 \end{pmatrix} = 4 \ x \begin{pmatrix} 3 \\ 2 \end{pmatrix}$$El vector resultante de la multiplicación es un múltiplo entero del vector original. Los eigenvectors de una matriz son todos aquellos vectores que, al multiplicarlos por dicha matriz, resultan en el mismo vector o en un múltiplo entero del mismo. Los eigenvectors tienen una serie de propiedades matemáticas específicas:
Los eigenvectors solo existen para matrices cuadradas y no para todas. En el caso de que una matriz n x n tenga eigenvectors, el número de ellos es n.
Si se escala un eigenvector antes de multiplicarlo por la matriz, se obtiene un múltiplo del mismo eigenvector. Esto se debe a que, si se escala un vector multiplicándolo por cierta cantidad, lo único que se consigue es cambiar su longitud pero la dirección es la misma.
Todos los eigenvectors de una matriz son perpendiculares (ortogonales) entre ellos, independientemente de las dimensiones que tengan.
Dada la propiedad de que multiplicar un eigenvector solo cambia su longitud pero no su naturaleza de eigenvector, es frecuente escalarlos de tal forma que su longitud sea 1. De este modo se consigue que todos ellos estén estandarizados. A continuación se muestra un ejemplo:
El eigenvector $\begin{pmatrix} 3 \\ 2 \end{pmatrix}$ tiene una longitud de $\sqrt{3^2 + 2^2} = \sqrt{13}$. Si se divide cada dimensión entre la longitud del vector, se obtiene el eigenvector estandarizado con longitud 1.
$$\begin{pmatrix} 3 \\ 2 \end{pmatrix} \div \sqrt{13} = \begin{pmatrix} 3/ \sqrt{13} \\ 2/ \sqrt{13} \end{pmatrix}$$Eigenvalue¶
Cuando se multiplica una matriz por alguno de sus eigenvectors se obtiene un múltiplo del vector original, es decir, el resultado es ese mismo vector multiplicado por un número. Al valor por el que se multiplica el eigenvector resultante se le conoce como eigenvalue. A todo eigenvector le corresponde un eigenvalue y viceversa.
En el método PCA, cada una de las componentes se corresponde con un eigenvector, y el orden de componente se establece por orden decreciente de eigenvalue. Así pues, la primera componente es el eigenvector con el eigenvalue más alto.
Interpretación geométrica de las componentes principales¶
Una forma intuitiva de entender el proceso de PCA es interpretar las componentes principales desde un punto de vista geométrico. Supóngase un conjunto de observaciones para las que se dispone de dos variables ($X_1$, $X_2$). El vector que define la primera componente principal ($Z_1$) sigue la dirección en la que las observaciones tienen más varianza (línea roja). La proyección de cada observación sobre esa dirección equivale al valor de la primera componente para dicha observación (principal component score, $z_{i1}$).
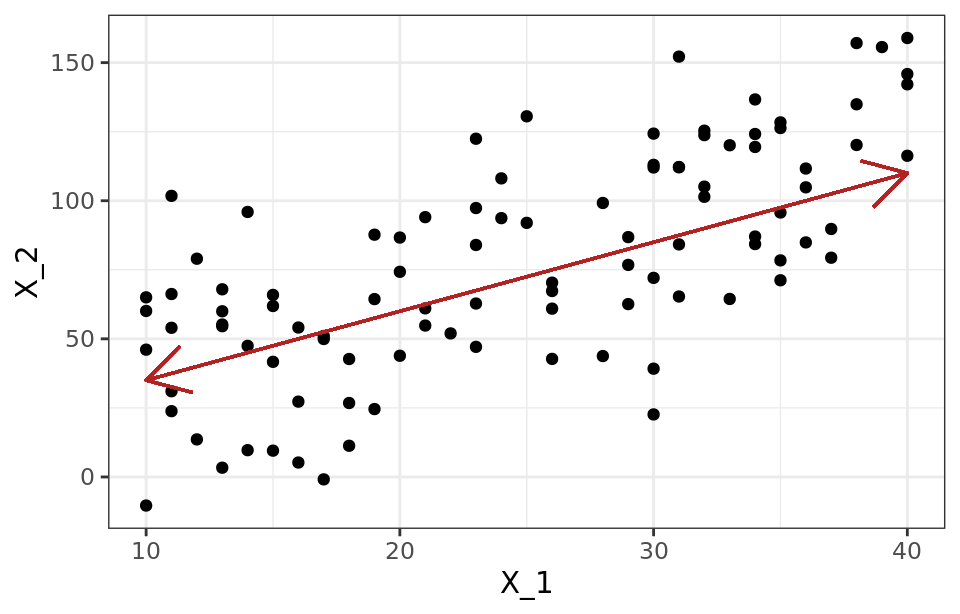
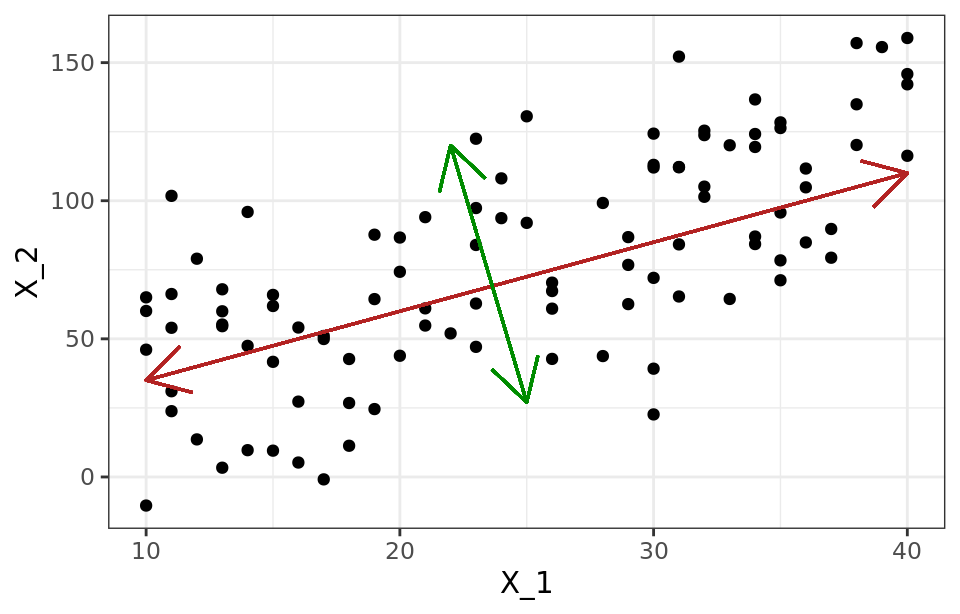
La segunda componente ($Z_2$) sigue la segunda dirección en la que los datos muestran mayor varianza y que no está correlacionada con la primera componente. La condición de no correlación entre componentes principales equivale a decir que sus direcciones son perpendiculares/ortogonales.
Cálculo de las componentes principales¶
Cada componente principal ($Z_i$) se obtiene por combinación lineal de las variables originales. Se pueden entender como nuevas variables obtenidas al combinar de una determinada forma las variables originales. La primera componente principal de un grupo de variables ($X_1$, $X_2$, ..., $X_p$) es la combinación lineal normalizada de dichas variables que tiene mayor varianza:
$$Z_1 = \phi_{11} X_1 + \phi_{21}X_2+ ... + \phi_{p1}X_p$$Que la combinación lineal sea normalizada implica que:
$$\displaystyle\sum_{j=1}^p \phi^{2}_{j1}= 1$$Los términos $\phi_{11}$, ..., $\phi_{1p}$ reciben en el nombre de loadings y son los que definen las componentes. Por ejemplo, $\phi_{11}$ es el loading de la variable $X_1$ de la primera componente principal. Los loadings pueden interpretarse como el peso/importancia que tiene cada variable en cada componente y, por lo tanto, ayudan a conocer que tipo de información recoge cada una de las componentes.
Dado un set de datos $X$ con n observaciones y p variables, el proceso a seguir para calcular la primera componente principal es:
Centrar las variables: se resta a cada valor la media de la variable a la que pertenece. Con esto se consigue que todas las variables tengan media cero.
Se resuelve un problema de optimización para encontrar el valor de los loadings con los que se maximiza la varianza. Una forma de resolver esta optimización es mediante el cálculo de eigenvector-eigenvalue de la matriz de covarianzas.
Una vez calculada la primera componente ($Z_1$), se calcula la segunda ($Z_2$) repitiendo el mismo proceso pero añadiendo la condición de que la combinación lineal no pude estar correlacionada con la primera componente. Esto equivale a decir que $Z_1$ y $Z_2$ tienen que ser perpendiculares. EL proceso se repite de forma iterativa hasta calcular todas las posibles componentes (min(n-1, p)) o hasta que se decida detener el proceso. El orden de importancia de las componentes viene dado por la magnitud del eigenvalue asociado a cada eigenvector.
Escalado de las variables¶
El proceso de PCA identifica las direcciones con mayor varianza. Como la varianza de una variable se mide en sus mismas unidades elevadas al cuadrado, si antes de calcular las componentes no se estandarizan todas las variables para que tengan media cero y desviación estándar de uno, aquellas variables cuya escala sea mayor dominarán al resto. De ahí que sea recomendable estandarizar siempre los datos.
Reproducibilidad de las componentes¶
El proceso de PCA estándar es determinista, genera siempre las mismas componentes principales, es decir, el valor de los loadings resultantes es el mismo. La única diferencia que puede darse es que el signo de todos los loadings esté invertido. Esto es así porque el vector de loadings determina la dirección de la componente, y dicha dirección es la misma independientemente del signo (la componente sigue una línea que se extiende en ambas direcciones). Del mismo modo, el valor específico de las componentes obtenido para cada observación (principal component scores) es siempre el mismo, a excepción del signo.
Influencia de outliers¶
Al trabajar con varianzas, el método PCA es muy sensible a outliers, por lo que es recomendable estudiar si los hay. La detección de valores atípicos con respecto a una determinada dimensión es algo relativamente sencillo de hacer mediante comprobaciones gráficas. Sin embargo, cuando se trata con múltiples dimensiones el proceso se complica. Por ejemplo, considérese un hombre que mide 2 metros y pesa 50 kg. Ninguno de los dos valores es atípico de forma individual, pero en conjunto se trataría de un caso muy excepcional.
Proporción de varianza explicada¶
Una de las preguntas más frecuentes que surge tras realizar un PCA es: ¿Cuánta información presente en el set de datos original se pierde al proyectar las observaciones en un espacio de menor dimensión? o lo que es lo mismo ¿Cuanta información es capaz de capturar cada una de las componentes principales obtenidas? Para contestar a estas preguntas se recurre a la proporción de varianza explicada por cada componente principal.
Asumiendo que las variables se han normalizado para tener media cero, la varianza total presente en el set de datos se define como
$$\displaystyle\sum_{j=1}^p Var(X_j) = \displaystyle\sum_{j=1}^p \frac{1}{n} \displaystyle\sum_{i=1}^n x^{2}_{ij}$$y la varianza explicada por la componente m es
$$\frac{1}{n} \sum_{i=1}^n z^{2}_{im} = \frac{1}{n} \sum_{i=1}^n \left( \sum_{j=1}^p \phi_{jm}x_{ij} \right)^2$$Por lo tanto, la proporción de varianza explicada por la componente m viene dada por el ratio
$$\frac{\sum_{i=1}^n \left( \sum_{j=1}^p \phi_{jm}x_{ij} \right)^2} {\sum_{j=1}^p \sum_{i=1}^n x^{2}_{ij}} $$Tanto la proporción de varianza explicada, como la proporción de varianza explicada acumulada, son dos valores de gran utilidad a la hora de decidir el número de componentes principales a utilizar en los análisis posteriores. Si se calculan todas las componentes principales de un set de datos, entonces, aunque transformada, se está almacenando toda la información presente en los datos originales. El sumatorio de la proporción de varianza explicada acumulada de todas las componentes es siempre 1.
Número óptimo de componentes principales¶
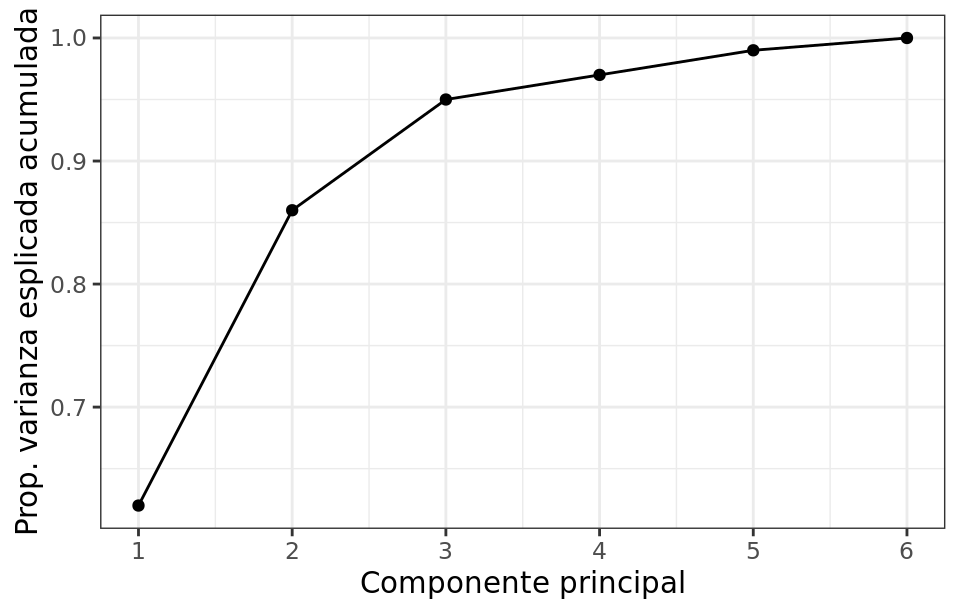
Por lo general, dada una matriz de datos de dimensiones n x p, el número de componentes principales que se pueden calcular es como máximo de n-1 o p (el menor de los dos valores es el limitante). Sin embargo, siendo el objetivo del PCA reducir la dimensionalidad, suelen ser de interés utilizar el número mínimo de componentes que resultan suficientes para explicar los datos. No existe una respuesta o método único que permita identificar cual es el número óptimo de componentes principales a utilizar. Una forma de proceder muy extendida consiste en evaluar la proporción de varianza explicada acumulada y seleccionar el número de componentes mínimo a partir del cual el incremento deja de ser sustancial.
Ejemplo PCA¶
Librerías¶
Las librerías utilizadas en este documento son:
# Tratamiento de datos
# ==============================================================================
import numpy as np
import pandas as pd
import statsmodels.api as sm
# Gráficos
# ==============================================================================
import matplotlib.pyplot as plt
import matplotlib.font_manager
from matplotlib import style
style.use('ggplot') or plt.style.use('ggplot')
# Preprocesado y modelado
# ==============================================================================
from sklearn.decomposition import PCA
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import scale
# Configuración warnings
# ==============================================================================
import warnings
warnings.filterwarnings('ignore')
Datos¶
El set de datos USArrests contiene el porcentaje de asaltos (Assault), asesinatos (Murder) y secuestros (Rape) por cada 100,000 habitantes para cada uno de los 50 estados de USA (1973). Además, también incluye el porcentaje de la población de cada estado que vive en zonas rurales (UrbanPoP).
# Lectura de datos
# ==============================================================================
USArrests = sm.datasets.get_rdataset("USArrests", "datasets")
datos = USArrests.data
datos.head(4)
| Murder | Assault | UrbanPop | Rape | |
|---|---|---|---|---|
| rownames | ||||
| Alabama | 13.2 | 236 | 58 | 21.2 |
| Alaska | 10.0 | 263 | 48 | 44.5 |
| Arizona | 8.1 | 294 | 80 | 31.0 |
| Arkansas | 8.8 | 190 | 50 | 19.5 |
Exploración inicial¶
Los dos principales aspectos a tener en cuenta cuando se quiere realizar un PCA es identificar el valor promedio y dispersión de las variables.
La media de las variables muestra que hay tres veces más secuestros que asesinatos y 8 veces más asaltos que secuestros.
print('----------------------')
print('Media de cada variable')
print('----------------------')
datos.mean(axis=0)
---------------------- Media de cada variable ----------------------
Murder 7.788 Assault 170.760 UrbanPop 65.540 Rape 21.232 dtype: float64
La varianza es muy distinta entre las variables, en el caso de Assault, la varianza es varios órdenes de magnitud superior al resto.
print('-------------------------')
print('Varianza de cada variable')
print('-------------------------')
datos.var(axis=0)
------------------------- Varianza de cada variable -------------------------
Murder 18.970465 Assault 6945.165714 UrbanPop 209.518776 Rape 87.729159 dtype: float64
Si no se estandarizan las variables para que tengan media cero y desviación estándar de uno antes de realizar el estudio PCA, la variable Assault, que tiene una media y dispersión muy superior al resto, dominará la mayoría de las componentes principales.
Modelo PCA¶
La clase sklearn.decomposition.PCA incorpora las principales funcionalidades que se necesitan a la hora de trabajar con modelos PCA. El argumento n_components determina el número de componentes calculados. Si se indica None, se calculan todas las posibles (min(filas, columnas) - 1).
Por defecto, PCA() centra los valores pero no los escala. Esto es importante ya que, si las variables tienen distinta dispersión, como en este caso, es necesario escalarlas. Una forma de hacerlo es combinar un StandardScaler() y un PCA() dentro de un pipeline. Para más información sobre el uso de pipelines consultar Pipeline y ColumnTransformer.
# Entrenamiento modelo PCA con escalado de los datos
# ==============================================================================
pca_pipe = make_pipeline(StandardScaler(), PCA())
pca_pipe.fit(datos)
# Se extrae el modelo entrenado del pipeline
modelo_pca = pca_pipe.named_steps['pca']
Interpretación¶
Una vez entrenado el objeto PCA, pude accederse a toda la información de las componentes creadas.
components_ contiene el valor de los loadings $\phi$ que definen cada componente (eigenvector). Las filas se corresponden con las componentes principals (ordenadas de mayor a menor varianza explicada). Las filas se corresponden con las variables de entrada.
# Se convierte el array a dataframe para añadir nombres a los ejes
# ==============================================================================
pd.DataFrame(
data = modelo_pca.components_,
columns = datos.columns,
index = ['PC1', 'PC2', 'PC3', 'PC4']
)
| Murder | Assault | UrbanPop | Rape | |
|---|---|---|---|---|
| PC1 | 0.535899 | 0.583184 | 0.278191 | 0.543432 |
| PC2 | -0.418181 | -0.187986 | 0.872806 | 0.167319 |
| PC3 | -0.341233 | -0.268148 | -0.378016 | 0.817778 |
| PC4 | -0.649228 | 0.743407 | -0.133878 | -0.089024 |
Analizar con detalle el vector de loadings que forma cada componente puede ayudar a interpretar qué tipo de información recoge cada una de ellas. Por ejemplo, la primera componente es el resultado de la siguiente combinación lineal de las variables originales:
$$\text{PC1} = 0.535899 \text{ Murder} + 0.583184 \text{ Assault} + 0.278191 \text{ UrbanPop} + 0.543432 \text{ Rape}$$Los pesos asignados en la primera componente a las variables Assault, Murder y Rape son aproximadamente iguales entre ellos y superiores al asignado a UrbanPoP. Esto significa que la primera componente recoge mayoritariamente la información correspondiente a los delitos. En la segunda componente, es la variable UrbanPoP es la que tiene con diferencia mayor peso, por lo que se corresponde principalmente con el nivel de urbanización del estado. Si bien en este ejemplo la interpretación de las componentes es bastante clara, no en todos los casos ocurre lo mismo, sobre todo a medida que aumenta el número de variables.
La influencia de las variables en cada componente analizarse visualmente con un gráfico de tipo heatmap.
# Heatmap componentes
# ==============================================================================
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(4, 2))
componentes = modelo_pca.components_
plt.imshow(componentes.T, cmap='viridis', aspect='auto')
plt.yticks(range(len(datos.columns)), datos.columns)
plt.xticks(range(len(datos.columns)), np.arange(modelo_pca.n_components_) + 1)
plt.grid(False)
plt.colorbar();
Una vez calculadas las componentes principales, se puede conocer la varianza explicada por cada una de ellas, la proporción respecto al total y la proporción de varianza acumulada. Esta información está almacenada en los atributos explained_variance_ y explained_variance_ratio_ del modelo.
# Porcentaje de varianza explicada por cada componente
# ==============================================================================
print('----------------------------------------------------')
print('Porcentaje de varianza explicada por cada componente')
print('----------------------------------------------------')
print(modelo_pca.explained_variance_ratio_)
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(6, 4))
ax.bar(
x = np.arange(modelo_pca.n_components_) + 1,
height = modelo_pca.explained_variance_ratio_
)
for x, y in zip(np.arange(len(datos.columns)) + 1, modelo_pca.explained_variance_ratio_):
label = round(y, 2)
ax.annotate(
label,
(x,y),
textcoords="offset points",
xytext=(0,10),
ha='center'
)
ax.set_xticks(np.arange(modelo_pca.n_components_) + 1)
ax.set_ylim(0, 1.1)
ax.set_title('Porcentaje de varianza explicada por cada componente')
ax.set_xlabel('Componente principal')
ax.set_ylabel('Por. varianza explicada');
---------------------------------------------------- Porcentaje de varianza explicada por cada componente ---------------------------------------------------- [0.62006039 0.24744129 0.0891408 0.04335752]
En este caso, la primera componente explica el 62% de la varianza observada en los datos y la segunda el 24.7%. Las dos últimas componentes no superan por separado el 1% de varianza explicada.
# Porcentaje de varianza explicada acumulada
# ==============================================================================
prop_varianza_acum = modelo_pca.explained_variance_ratio_.cumsum()
print('------------------------------------------')
print('Porcentaje de varianza explicada acumulada')
print('------------------------------------------')
print(prop_varianza_acum)
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(6, 4))
ax.plot(
np.arange(len(datos.columns)) + 1,
prop_varianza_acum,
marker = 'o'
)
for x, y in zip(np.arange(len(datos.columns)) + 1, prop_varianza_acum):
label = round(y, 2)
ax.annotate(
label,
(x,y),
textcoords="offset points",
xytext=(0,10),
ha='center'
)
ax.set_ylim(0, 1.1)
ax.set_xticks(np.arange(modelo_pca.n_components_) + 1)
ax.set_title('Porcentaje de varianza explicada acumulada')
ax.set_xlabel('Componente principal')
ax.set_ylabel('Por. varianza acumulada');
------------------------------------------ Porcentaje de varianza explicada acumulada ------------------------------------------ [0.62006039 0.86750168 0.95664248 1. ]
Si se empleasen únicamente las dos primeras componentes se conseguiría explicar el 87% de la varianza observada.
Transformación¶
Una vez entrenado el modelo, con el método transform() se puede reducir la dimensionalidad de nuevas observaciones proyectándolas en el espacio definido por las componentes.
# Proyección de las observaciones de entrenamiento
# ==============================================================================
proyecciones = pca_pipe.transform(X=datos)
proyecciones = pd.DataFrame(
proyecciones,
columns = ['PC1', 'PC2', 'PC3', 'PC4'],
index = datos.index
)
proyecciones.head()
| PC1 | PC2 | PC3 | PC4 | |
|---|---|---|---|---|
| rownames | ||||
| Alabama | 0.985566 | -1.133392 | -0.444269 | -0.156267 |
| Alaska | 1.950138 | -1.073213 | 2.040003 | 0.438583 |
| Arizona | 1.763164 | 0.745957 | 0.054781 | 0.834653 |
| Arkansas | -0.141420 | -1.119797 | 0.114574 | 0.182811 |
| California | 2.523980 | 1.542934 | 0.598557 | 0.341996 |
La transformación es el resultado de multiplicar los vectores que definen cada componente con el valor de las variables. Puede calcularse de forma manual:
proyecciones = np.dot(modelo_pca.components_, scale(datos).T)
proyecciones = pd.DataFrame(proyecciones, index = ['PC1', 'PC2', 'PC3', 'PC4'])
proyecciones = proyecciones.transpose().set_index(datos.index)
proyecciones.head()
| PC1 | PC2 | PC3 | PC4 | |
|---|---|---|---|---|
| rownames | ||||
| Alabama | 0.985566 | -1.133392 | -0.444269 | -0.156267 |
| Alaska | 1.950138 | -1.073213 | 2.040003 | 0.438583 |
| Arizona | 1.763164 | 0.745957 | 0.054781 | 0.834653 |
| Arkansas | -0.141420 | -1.119797 | 0.114574 | 0.182811 |
| California | 2.523980 | 1.542934 | 0.598557 | 0.341996 |
Reconstrucción¶
Puede revertirse la transformación y reconstruir el valor inicial con el método inverse_transform(). Es importante tener en cuenta que, la reconstrucción, solo será completa si se han incluido todas las componentes.
# Recostruccion de las proyecciones
# ==============================================================================
recostruccion = pca_pipe.inverse_transform(X=proyecciones)
recostruccion = pd.DataFrame(
recostruccion,
columns = datos.columns,
index = datos.index
)
print('------------------')
print('Valores originales')
print('------------------')
display(recostruccion.head())
print('---------------------')
print('Valores reconstruidos')
print('---------------------')
display(datos.head())
------------------ Valores originales ------------------
| Murder | Assault | UrbanPop | Rape | |
|---|---|---|---|---|
| rownames | ||||
| Alabama | 13.2 | 236.0 | 58.0 | 21.2 |
| Alaska | 10.0 | 263.0 | 48.0 | 44.5 |
| Arizona | 8.1 | 294.0 | 80.0 | 31.0 |
| Arkansas | 8.8 | 190.0 | 50.0 | 19.5 |
| California | 9.0 | 276.0 | 91.0 | 40.6 |
--------------------- Valores reconstruidos ---------------------
| Murder | Assault | UrbanPop | Rape | |
|---|---|---|---|---|
| rownames | ||||
| Alabama | 13.2 | 236 | 58 | 21.2 |
| Alaska | 10.0 | 263 | 48 | 44.5 |
| Arizona | 8.1 | 294 | 80 | 31.0 |
| Arkansas | 8.8 | 190 | 50 | 19.5 |
| California | 9.0 | 276 | 91 | 40.6 |
Ejemplo Principal Components Regression¶
El método Principal Components Regression PCR consiste en ajustar un modelo de regresión lineal por mínimos cuadrados empleando como predictores las componentes generadas a partir de un Principal Component Analysis (PCA). De esta forma, con un número reducido de componentes se puede explicar la mayor parte de la varianza de los datos.
En los estudios observacionales, es frecuente disponer de un número elevado de variables que se pueden emplear como predictores, sin embargo, esto no implica necesariamente que se disponga de mucha información. Si las variables están correlacionadas entre ellas, la información que aportan es redundante y además, se incumple la condición de no colinealidad necesaria en la regresión por mínimos cuadrados. Dado que el PCA es útil eliminando información redundante, si se emplean como predictores las componentes principales, se puede mejorar el modelo de regresión. Es importante tener en cuenta que, si bien el Principal Components Regression reduce el número de predictores del modelo, no se puede considerar como un método de selección de variables ya que todas ellas se necesitan para el cálculo de las componentes. La identificación del número óptimo de componentes principales que se emplean como predictores en PCR puede identificarse por validación cruzada.
Librerías¶
Las librerías utilizadas en este ejemplo son:
# Tratamiento de datos
# ==============================================================================
import numpy as np
import pandas as pd
import statsmodels.api as sm
# Gráficos
# ==============================================================================
import matplotlib.pyplot as plt
import matplotlib.font_manager
from matplotlib import style
style.use('ggplot') or plt.style.use('ggplot')
# Preprocesado y modelado
# ==============================================================================
from sklearn.decomposition import PCA
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import KFold
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import root_mean_squared_error
import multiprocessing
# Configuración warnings
# ==============================================================================
import warnings
warnings.filterwarnings('once')
Datos¶
El departamento de calidad de una empresa de alimentación se encarga de medir el contenido en grasa de la carne que comercializa. Este estudio se realiza mediante técnicas de analítica química, un proceso relativamente costoso en tiempo y recursos. Una alternativa que permitiría reducir costes y optimizar tiempo es emplear un espectrofotómetro (instrumento capaz de detectar la absorbancia que tiene un material a diferentes tipos de luz en función de sus características) e inferir el contenido en grasa a partir de sus medidas.
Antes de dar por válida esta nueva técnica, la empresa necesita comprobar qué margen de error tiene respecto al análisis químico. Para ello, se mide el espectro de absorbancia a 100 longitudes de onda en 215 muestras de carne, cuyo contenido en grasa se obtiene también por análisis químico, y se entrena un modelo con el objetivo de predecir el contenido en grasa a partir de los valores dados por el espectrofotómetro.
Los datos meatspec.csv empleados en este ejemplo se han obtenido del magnífico libro Linear Models with R, Second Edition.
# Datos
# ==============================================================================
datos = pd.read_csv('meatspec.csv')
datos = datos.drop(columns = datos.columns[0])
El set de datos contiene 101 columnas. Las 100 primeras, nombradas como $V1$, ..., $V100$ recogen el valor de absorbancia para cada una de las 100 longitudes de onda analizadas (predictores), y la columna fat el contenido en grasa medido por técnicas químicas (variable respuesta).
Muchas de las variables están altamente correlacionadas (correlación absoluta > 0.8), lo que supone un problema a la hora de emplear modelos de regresión lineal.
# Correlación entre columnas numéricas
# ==============================================================================
def tidy_corr_matrix(corr_mat):
'''
Función para convertir una matriz de correlación de pandas en formato tidy
'''
corr_mat = corr_mat.stack().reset_index()
corr_mat.columns = ['variable_1','variable_2','r']
corr_mat = corr_mat.loc[corr_mat['variable_1'] != corr_mat['variable_2'], :]
corr_mat['abs_r'] = np.abs(corr_mat['r'])
corr_mat = corr_mat.sort_values('abs_r', ascending=False)
return(corr_mat)
corr_matrix = datos.select_dtypes(include=['float64', 'int']) \
.corr(method='pearson')
display(tidy_corr_matrix(corr_matrix).head(5))
| variable_1 | variable_2 | r | abs_r | |
|---|---|---|---|---|
| 1019 | V11 | V10 | 0.999996 | 0.999996 |
| 919 | V10 | V11 | 0.999996 | 0.999996 |
| 1121 | V12 | V11 | 0.999996 | 0.999996 |
| 1021 | V11 | V12 | 0.999996 | 0.999996 |
| 917 | V10 | V9 | 0.999996 | 0.999996 |
Modelos¶
Se ajustan dos modelos lineales, uno con todos los predictores y otro con solo algunas de las componentes obtenidas por PCA, con el objetivo de identificar cuál de ellos es capaz de predecir mejor el contenido en grasa de la carne en función de las señales registradas por el espectrofotómetro.
Para poder evaluar la capacidad predictiva de cada modelo, se dividen las observaciones disponibles en dos grupos: uno de entrenamiento (70%) y otro de test (30%).
# División de los datos en train y test
# ==============================================================================
X = datos.drop(columns='fat')
y = datos['fat']
X_train, X_test, y_train, y_test = train_test_split(
X,
y,
train_size = 0.7,
random_state = 1234,
shuffle = True
)
Mínimos cuadrados (OLS)¶
# Creación y entrenamiento del modelo
# ==============================================================================
modelo = LinearRegression()
modelo.fit(X = X_train, y = y_train)
LinearRegression()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
Parameters
| fit_intercept | True | |
| copy_X | True | |
| tol | 1e-06 | |
| n_jobs | None | |
| positive | False |
# Predicciones test
# ==============================================================================
predicciones = modelo.predict(X=X_test)
predicciones = predicciones.flatten()
# Error de test del modelo
# ==============================================================================
rmse_ols = root_mean_squared_error(
y_true = y_test,
y_pred = predicciones
)
print("")
print(f"El error (rmse) de test es: {rmse_ols}")
El error (rmse) de test es: 3.839667585624623
Las predicciones del modelo final se alejan en promedio 3.84 unidades del valor real.
PCR¶
Para combinar PCA con regresión lineal, se crea un pipeline que combine ambos procesos. Dado que no se puede conocer a priori el número de componentes óptimo, se recurre a validación cruzada.
# Entrenamiento modelo de regresión precedido por PCA con escalado
# ==============================================================================
pipe_modelado = make_pipeline(StandardScaler(), PCA(), LinearRegression())
pipe_modelado.fit(X=X_train, y=y_train)
Pipeline(steps=[('standardscaler', StandardScaler()), ('pca', PCA()),
('linearregression', LinearRegression())])In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
Parameters
| steps | [('standardscaler', ...), ('pca', ...), ...] | |
| transform_input | None | |
| memory | None | |
| verbose | False |
Parameters
| copy | True | |
| with_mean | True | |
| with_std | True |
Parameters
| n_components | None | |
| copy | True | |
| whiten | False | |
| svd_solver | 'auto' | |
| tol | 0.0 | |
| iterated_power | 'auto' | |
| n_oversamples | 10 | |
| power_iteration_normalizer | 'auto' | |
| random_state | None |
Parameters
| fit_intercept | True | |
| copy_X | True | |
| tol | 1e-06 | |
| n_jobs | None | |
| positive | False |
Primero se evalua el modelo si se incluyen todas las componentes.
# Predicciones test
# ==============================================================================
predicciones = pipe_modelado.predict(X=X_test)
predicciones = predicciones.flatten()
# Error de test del modelo
# ==============================================================================
rmse_pcr = root_mean_squared_error(
y_true = y_test,
y_pred = predicciones
)
print("")
print(f"El error (rmse) de test es: {rmse_pcr}")
El error (rmse) de test es: 3.8396675856416405
# Grid de hiperparámetros evaluados
# ==============================================================================
param_grid = {'pca__n_components': [1, 2, 4, 6, 8, 10, 15, 20, 30, 50]}
# Búsqueda por grid search con validación cruzada
# ==============================================================================
grid = GridSearchCV(
estimator = pipe_modelado,
param_grid = param_grid,
scoring = 'neg_root_mean_squared_error',
n_jobs = multiprocessing.cpu_count() - 1,
cv = KFold(n_splits=5),
refit = True,
verbose = 0,
return_train_score = True
)
grid.fit(X = X_train, y = y_train)
# Resultados
# ==============================================================================
resultados = pd.DataFrame(grid.cv_results_)
resultados.filter(regex = '(param.*|mean_t|std_t)') \
.drop(columns = 'params') \
.sort_values('mean_test_score', ascending = False) \
.head(3)
| param_pca__n_components | mean_test_score | std_test_score | mean_train_score | std_train_score | |
|---|---|---|---|---|---|
| 8 | 30 | -2.710551 | 1.104449 | -1.499120 | 0.071778 |
| 5 | 10 | -2.791629 | 0.416056 | -2.448375 | 0.109985 |
| 6 | 15 | -2.842055 | 0.585350 | -2.247184 | 0.099187 |
# Gráfico resultados validación cruzada para cada hiperparámetro
# ==============================================================================
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(7, 3.84), sharey=True)
resultados.plot('param_pca__n_components', 'mean_train_score', ax=ax)
resultados.plot('param_pca__n_components', 'mean_test_score', ax=ax)
ax.fill_between(resultados.param_pca__n_components.astype(float),
resultados['mean_train_score'] + resultados['std_train_score'],
resultados['mean_train_score'] - resultados['std_train_score'],
alpha=0.2)
ax.fill_between(resultados.param_pca__n_components.astype(float),
resultados['mean_test_score'] + resultados['std_test_score'],
resultados['mean_test_score'] - resultados['std_test_score'],
alpha=0.2)
ax.legend()
ax.set_title('Evolución del error CV')
ax.set_ylabel('neg_root_mean_squared_error');
# Mejores hiperparámetros por validación cruzada
# ==============================================================================
print("----------------------------------------")
print("Mejores hiperparámetros encontrados (cv)")
print("----------------------------------------")
print(grid.best_params_, ":", grid.best_score_, grid.scoring)
----------------------------------------
Mejores hiperparámetros encontrados (cv)
----------------------------------------
{'pca__n_components': 30} : -2.7105505991489536 neg_root_mean_squared_error
Los resultados de validación cruzada muestran que, el mejor modelo, se obtiene empleando las 30 primeras componentes. Sin embargo, teniendo en cuenta la evolución del error y su intervalo, a partir de las 5 componentes no se consiguen mejoras significativas. Siguiendo el principio de parsimonia, el mejor modelo es el que emplea únicamente las 5 primeras componentes. Se reentrena el modelo indicando esta configuración.
# Entrenamiento modelo de regresión precedido por PCA con escalado
# ==============================================================================
pipe_modelado = make_pipeline(StandardScaler(), PCA(n_components=5), LinearRegression())
pipe_modelado.fit(X=X_train, y=y_train)
Pipeline(steps=[('standardscaler', StandardScaler()),
('pca', PCA(n_components=5)),
('linearregression', LinearRegression())])In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
Parameters
| steps | [('standardscaler', ...), ('pca', ...), ...] | |
| transform_input | None | |
| memory | None | |
| verbose | False |
Parameters
| copy | True | |
| with_mean | True | |
| with_std | True |
Parameters
| n_components | 5 | |
| copy | True | |
| whiten | False | |
| svd_solver | 'auto' | |
| tol | 0.0 | |
| iterated_power | 'auto' | |
| n_oversamples | 10 | |
| power_iteration_normalizer | 'auto' | |
| random_state | None |
Parameters
| fit_intercept | True | |
| copy_X | True | |
| tol | 1e-06 | |
| n_jobs | None | |
| positive | False |
Finalmente, se evalúa el modelo con los datos de test.
# Predicciones test
# ==============================================================================
predicciones = pipe_modelado.predict(X=X_test)
predicciones = predicciones.flatten()
# Error de test del modelo
# ==============================================================================
rmse_pcr = root_mean_squared_error(
y_true = y_test,
y_pred = predicciones
)
print("")
print(f"El error (rmse) de test es: {rmse_pcr}")
El error (rmse) de test es: 3.359334804522664
Comparación¶
Empleando las cinco primeras componentes del PCA como predictores en lugar de las variables originales, se consigue reducir el root mean squared error de 3.84 a 3.36.
Información de sesión¶
import session_info
session_info.show(html=False)
----- matplotlib 3.10.1 numpy 2.2.6 pandas 2.3.1 session_info v1.0.1 sklearn 1.7.1 statsmodels 0.14.4 ----- IPython 9.1.0 jupyter_client 8.6.3 jupyter_core 5.7.2 jupyterlab 4.4.5 notebook 7.4.5 ----- Python 3.12.9 | packaged by Anaconda, Inc. | (main, Feb 6 2025, 18:56:27) [GCC 11.2.0] Linux-6.14.0-28-generic-x86_64-with-glibc2.39 ----- Session information updated at 2025-08-20 23:06
Bibliografía¶
Introduction to Machine Learning with Python: A Guide for Data Scientists
Python Data Science Handbook by Jake VanderPlas
Linear Models with R by Julian J.Faraway
An Introduction to Statistical Learning: with Applications in R (Springer Texts in Statistics)
OpenIntro Statistics: Fourth Edition by David Diez, Mine Çetinkaya-Rundel, Christopher Barr
Points of Significance Principal component analysis by Jake Lever, Martin Krzywinski & Naomi Altman
Instrucciones para citar¶
¿Cómo citar este documento?
Si utilizas este documento o alguna parte de él, te agradecemos que lo cites. ¡Muchas gracias!
Análisis de componentes principales PCA con Python por Joaquín Amat Rodrigo, disponible bajo una licencia Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0 DEED) en https://cienciadedatos.net/documentos/py19-pca-python.html
¿Te ha gustado el artículo? Tu ayuda es importante
Tu contribución me ayudará a seguir generando contenido divulgativo gratuito. ¡Muchísimas gracias! 😊
Este documento creado por Joaquín Amat Rodrigo tiene licencia Attribution-NonCommercial-ShareAlike 4.0 International.
Se permite:
-
Compartir: copiar y redistribuir el material en cualquier medio o formato.
-
Adaptar: remezclar, transformar y crear a partir del material.
Bajo los siguientes términos:
-
Atribución: Debes otorgar el crédito adecuado, proporcionar un enlace a la licencia e indicar si se realizaron cambios. Puedes hacerlo de cualquier manera razonable, pero no de una forma que sugiera que el licenciante te respalda o respalda tu uso.
-
No-Comercial: No puedes utilizar el material para fines comerciales.
-
Compartir-Igual: Si remezclas, transformas o creas a partir del material, debes distribuir tus contribuciones bajo la misma licencia que el original.

