Modelos de forecasting globales: modelado de múltiples series temporales con machine learning
Más sobre forecasting en: cienciadedatos.net
- Forecasting series temporales con machine learning
- Modelos ARIMA y SARIMAX
- Forecasting series temporales con gradient boosting: XGBoost, LightGBM y CatBoost
- Global Forecasting: Multi-series forecasting
- Forecasting de la demanda eléctrica con machine learning
- Forecasting con deep learning
- Forecasting de visitas a página web con machine learning
- Forecasting del precio de Bitcoin
- Forecasting probabilístico
- Forecasting de demanda intermitente
- Reducir el impacto del Covid en modelos de forecasting
- Modelar series temporales con tendencia utilizando modelos de árboles
Modelos de forecasting globales¶
En los modelos de series individuales (Local Forecasting Model), una única serie temporal se modela como una combinación lineal o no lineal de sus valores pasados (lags) y, opcionalmente, variables exógenas. Aunque este método proporciona una comprensión exhaustiva de cada serie, su escalabilidad puede verse comprometida cuando se dispone de un gran número de series.
Los modelos globales multiserie (Global Forecasting Model) consisten en un único modelo que tiene en cuenta varias series temporales de forma simultánea. Intentan captar los patrones básicos que rigen las series, mitigando así el ruido potencial que pueda introducir cada serie. Este enfoque es eficiente desde el punto de vista computacional, es fácil de mantener y puede conseguir mayor generalización, aunque potencialmente a costa de sacrificar cierta resolución individual. Se pueden distinguir dos estrategias de modelos de previsión global:
Múltiples series temporales independientes
En esta situación, cada serie temporal es independiente de las demás o, dicho de otro modo, los valores pasados de una serie no se utilizan como predictores de las otras series. ¿Por qué es útil entonces modelar todo junto? Aunque las series no dependen unas de otras, pueden seguir el mismo patrón intrínseco en cuanto a sus valores pasados y futuros. Por ejemplo, en una misma tienda, las ventas de los productos A y B pueden no estar relacionadas, pero siguen la misma dinámica, la de la tienda.
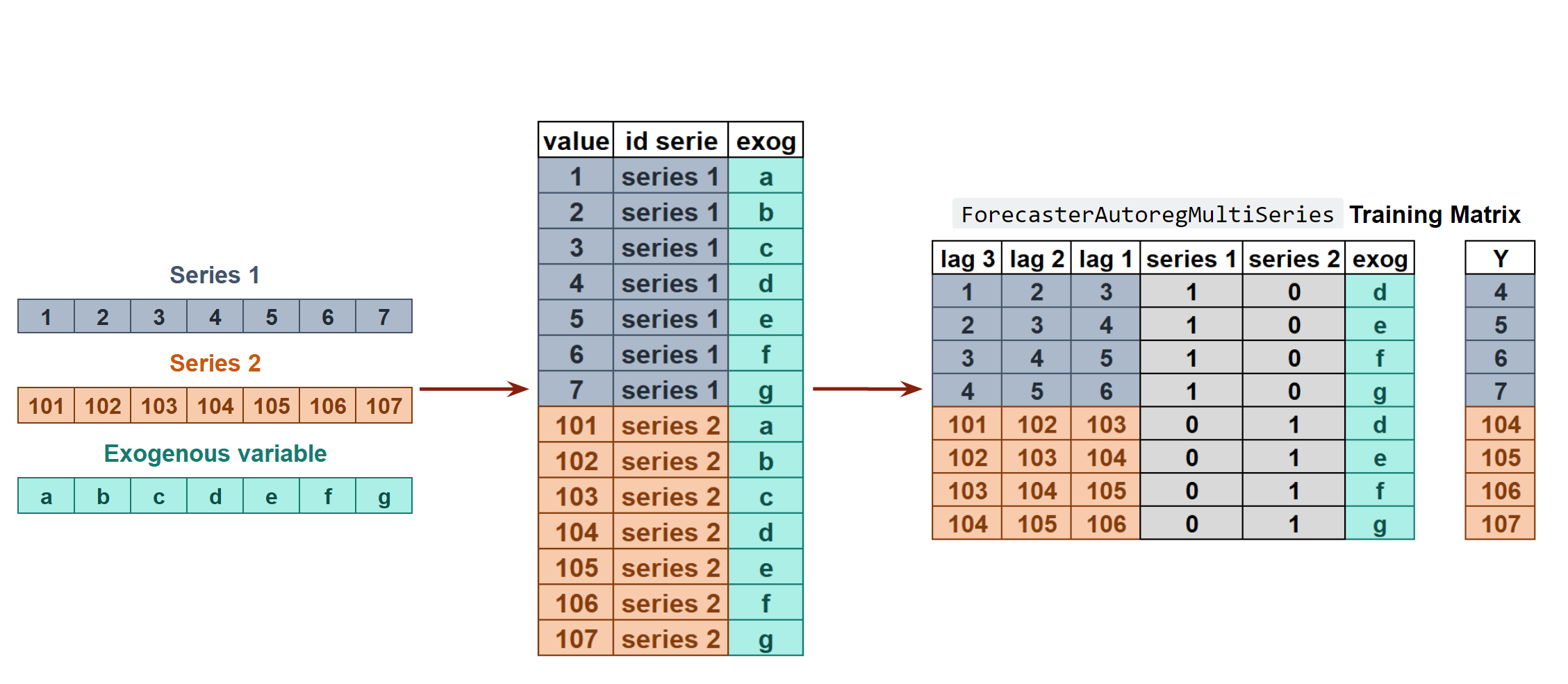
Para predecir los siguientes n steps, se sigue una estrategia recurisva, recursive multi-step forecasting.
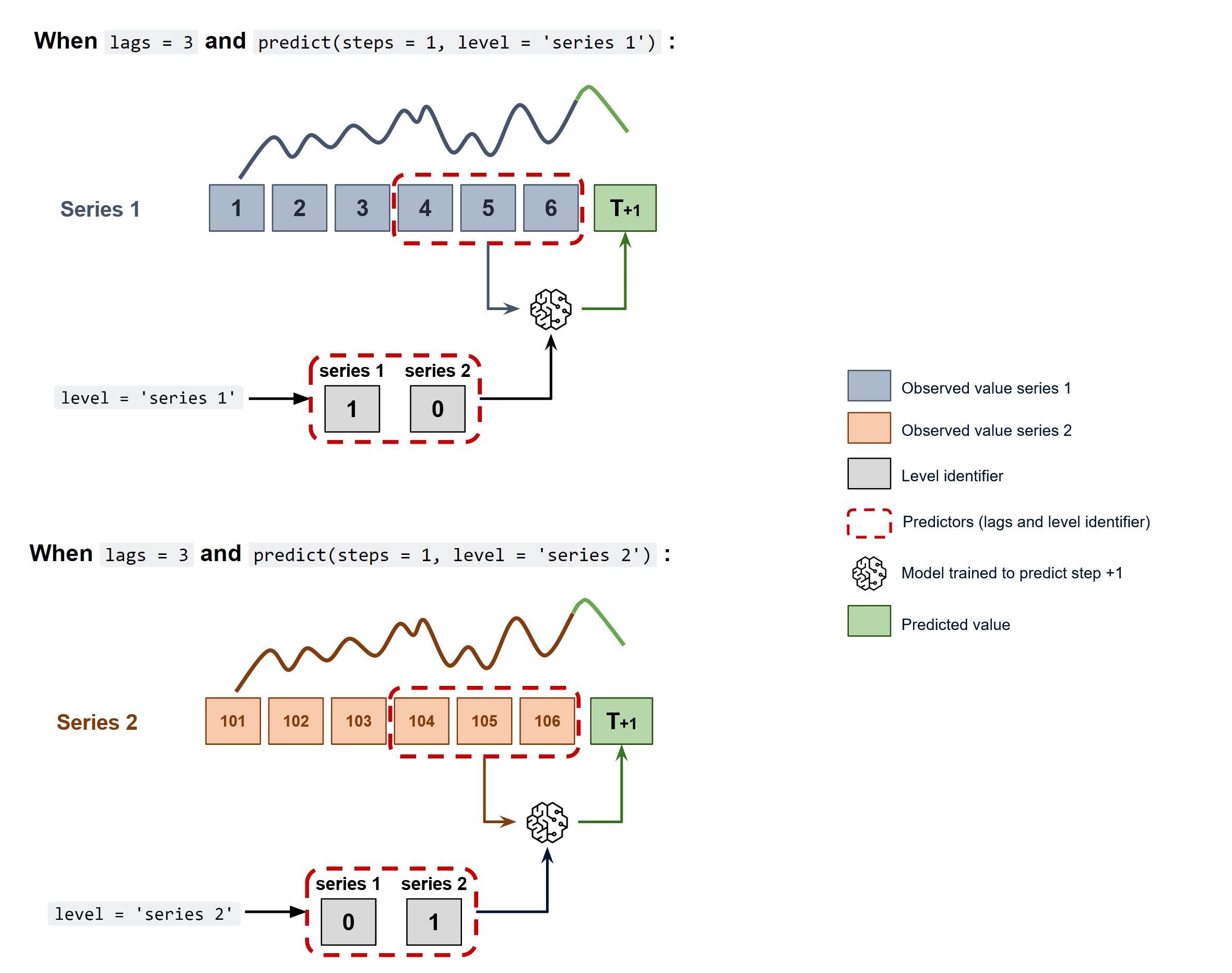
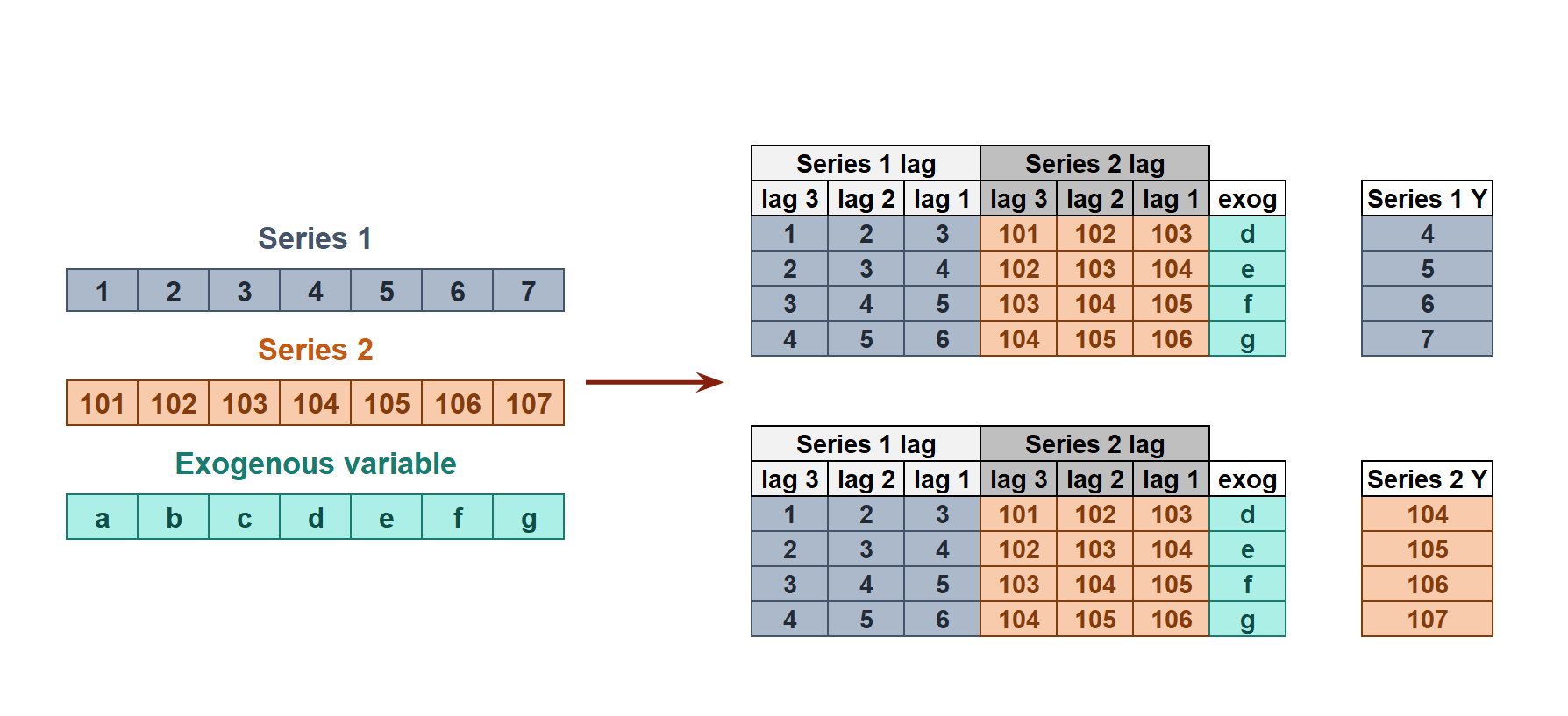
Múltiples series temporales dependientes
Todas las series se modelan teniendo en cuenta que cada serie temporal depende no sólo de sus valores pasados, sino también de los valores pasados de las demás series. Se espera que el modelo no sólo aprenda la información de cada serie por separado, sino que también las relacione. Por ejemplo, las mediciones realizadas por todos los sensores (caudal, temperatura, presión...) instalados en una máquina industrial como un compresor. Series temporales multivariantes user guide.
🖉 Nota
La claseForecasterAutoregMultiSeries y ForecasterAutoregMultiSeriesCustom permite modelar series temporales independientes. API Reference
La clase ForecasterAutoregMultivariate permite modelar series temporales dependientes. API Reference
Ventajas y limitaciones¶
Los modelos de forecasting globales no siempre superan al modelado individual de cada serie. Cuál de funciona mejor depende en gran medida de las características del caso de uso al que se aplican. Sin embargo, conviene tener en cuenta la siguiente heurística:
Ventajas de los modelos multiseries
Es más fácil mantener y controlar un solo modelo que varios.
Dado que todas las series temporales se combinan durante el entrenamiento, cuando las series sean cortas (pocos datos) el modelo tendrá una mayor capacidad de aprendizaje al disponer de más observaciones.
Al combinar múltiples series temporales, el modelo puede aprender patrones más generalizables.
Desventajas de los modelos multiseries
Si las series no siguen la misma dinámica interna, el modelo puede aprender un patrón que no represente a ninguna de ellas.
Las series pueden enmascararse unas a otras, por lo que el modelo puede no predecirlas todas con el mismo rendimiento.
Es más exigente desde el punto de vista computacional (tiempo y recursos) entrenar y realizar backtesting de un modelo grande que de varios pequeños.
Series con la misma longitud¶
El objetivo de este estudio es comparar los resultados obtenidos por un modelo multiserie frente a la utilización de un modelo diferente para cada serie.
Los datos se han obtenido de Store Item Demand Forecasting Challenge. Este dataset contiene 913.000 transacciones de ventas desde el 2013-01-01 hasta el 2017-12-31 para 50 productos (SKU) en 10 tiendas. El objetivo es predecir las ventas de los próximos 7 días de 50 artículos diferentes en una tienda utilizando el historial disponible de 5 años.
Librerías¶
# Manipulación de datos
# ==============================================================================
import sys
import os
import warnings
import numpy as np
import pandas as pd
# Gráficos
# ==============================================================================
import matplotlib.pyplot as plt
from tqdm.notebook import tqdm
from statsmodels.graphics.tsaplots import plot_acf
# Modelado y Forecasting
# ==============================================================================
import sklearn
import skforecast
from sklearn.preprocessing import StandardScaler
from sklearn.feature_selection import RFECV
from sklearn.ensemble import HistGradientBoostingRegressor
from skforecast.ForecasterAutoregMultiSeries import ForecasterAutoregMultiSeries
from skforecast.ForecasterAutoreg import ForecasterAutoreg
from skforecast.model_selection import backtesting_forecaster
from skforecast.model_selection import bayesian_search_forecaster
from skforecast.model_selection_multiseries import backtesting_forecaster_multiseries
from skforecast.model_selection_multiseries import bayesian_search_forecaster_multiseries
from skforecast.model_selection_multiseries import select_features_multiseries
from skforecast.plot import set_dark_theme
from skforecast.preprocessing import series_long_to_dict
from skforecast.preprocessing import exog_long_to_dict
# Warnings
# ==============================================================================
warnings.filterwarnings('once')
color = '\033[1m\033[38;5;208m'
print(f"{color}Versión skforecast: {skforecast.__version__}")
print(f"{color}Versión scikit-learn: {sklearn.__version__}")
print(f"{color}Versión pandas: {pd.__version__}")
print(f"{color}Versión numpy: {np.__version__}")
Datos¶
# Lectura de datos
# ======================================================================================
data = pd.read_csv('./train_stores_kaggle.csv')
display(data)
print(f"Shape: {data.shape}")
# Preparación datos
# ======================================================================================
selected_store = 2 # Seleccionar una tienda
selected_items = data.item.unique()
data = data[(data['store'] == selected_store) & (data['item'].isin(selected_items))].copy()
data['date'] = pd.to_datetime(data['date'], format='%Y-%m-%d')
data = pd.pivot_table(
data = data,
values = 'sales',
index = 'date',
columns = 'item'
)
data.columns.name = None
data.columns = [f"item_{col}" for col in data.columns]
data = data.asfreq('1D')
data = data.sort_index()
data.head(4)
El dataset se divide en 3 particiones: una para el entrenamiento, otra para la validación y otra para test.
# Separación datos train-validation-test
# ======================================================================================
end_train = '2016-05-31 23:59:00'
end_val = '2017-05-31 23:59:00'
data_train = data.loc[:end_train, :].copy()
data_val = data.loc[end_train:end_val, :].copy()
data_test = data.loc[end_val:, :].copy()
print(f"Fechas train : {data_train.index.min()} --- {data_train.index.max()} (n={len(data_train)})")
print(f"Fechas validación : {data_val.index.min()} --- {data_val.index.max()} (n={len(data_val)})")
print(f"Fechas test : {data_test.index.min()} --- {data_test.index.max()} (n={len(data_test)})")
Se representan cuatro de las series para comprender sus tendencias y patrones. Se recomienda al lector que grafique más de ellas para comprenderlas en profundidad.
# Gráfico series temporales
# ======================================================================================
set_dark_theme()
fig, axs = plt.subplots(4, 1, figsize=(7, 5), sharex=True)
data.iloc[:, :4].plot(
legend = True,
subplots = True,
title = 'Ventas de la tienda 2',
ax = axs,
)
for ax in axs:
ax.axvline(pd.to_datetime(end_train) , color='white', linestyle='--', linewidth=1.5)
ax.axvline(pd.to_datetime(end_val) , color='white', linestyle='--', linewidth=1.5)
fig.tight_layout();
# Gráficos de autocorrelación
# ======================================================================================
fig, axes = plt.subplots(nrows=4, ncols=1, figsize=(7, 5), sharex=True)
axes = axes.flat
for i, col in enumerate(data.columns[:4]):
plot_acf(data[col], ax=axes[i], lags=7*5)
axes[i].set_ylim(-1, 1.1)
axes[i].set_title(f'{col}', fontsize=10)
fig.tight_layout()
plt.show()
Los gráficos de autocorrelación muestran una clara asociación entre las ventas de un día y las del mismo día una semana antes. Este tipo de correlación es un indicio de que los modelos autorregresivos pueden funcionar bien. También hay una estacionalidad semanal común entre las series. Cuanto más similar sea la dinámica entre las series, más probable será que el modelo multiseries aprenda patrones útiles.
Forecasting individual para cada item¶
Se entrena un modelo diferente (Gradient Boosting Machine) para cada artículo de la tienda y se estima su error medio absoluto mediante backtesting.
# Entrenar y realizar backtesting de un modelo para cada item
# ======================================================================================
items = []
mae_values = []
predictions = {}
for i, item in enumerate(tqdm(data.columns)):
# Definir el forecaster
forecaster = ForecasterAutoreg(
regressor = HistGradientBoostingRegressor(random_state=123),
lags = 14,
transformer_y = StandardScaler()
)
# Backtesting forecaster
metric, preds = backtesting_forecaster(
forecaster = forecaster,
y = data[item],
initial_train_size = len(data_train) + len(data_val),
steps = 7,
metric = 'mean_absolute_error',
refit = False,
fixed_train_size = False,
verbose = False,
show_progress = False
)
items.append(item)
mae_values.append(metric.at[0, 'mean_absolute_error'])
predictions[item] = preds
# Resultados
uni_series_mae = pd.Series(
data = mae_values,
index = items,
name = 'uni_series_mae'
)
Modelo global: Forecasting multiseries¶
Se entrena un único modelo con todas las series simultáneamente. En el método predict, y en el proceso de backtesting se indica el level para se desea realizar las predicciones. Si level es None, entonces se predicen todas las series disponibles.
# Entrenamiento y backtesting con un único modelo para todos los items
# ======================================================================================
items = list(data.columns)
# Definir el forecaster
forecaster_ms = ForecasterAutoregMultiSeries(
regressor = HistGradientBoostingRegressor(random_state=8523),
lags = 14,
encoding = 'ordinal',
transformer_series = StandardScaler(),
)
# Backtesting forecaster para todos los items
multi_series_mae, predictions_ms = backtesting_forecaster_multiseries(
forecaster = forecaster_ms,
series = data,
levels = items,
steps = 7,
metric = 'mean_absolute_error',
add_aggregated_metric = False,
initial_train_size = len(data_train) + len(data_val),
refit = False,
fixed_train_size = False,
verbose = False,
show_progress = True
)
# Resultados
display(multi_series_mae.head(3))
print('')
display(predictions_ms.head(3))
Comparación¶
# Diferencia de la métrica de backtesting para cada item
# ======================================================================================
multi_series_mae = multi_series_mae.set_index('levels')
multi_series_mae.columns = ['multi_series_mae']
results = pd.concat((uni_series_mae, multi_series_mae), axis = 1)
results['improvement'] = results.eval('uni_series_mae - multi_series_mae')
results['improvement_(%)'] = 100 * results.eval('(uni_series_mae - multi_series_mae) / uni_series_mae')
results = results.round(2)
results.style.bar(subset=['improvement_(%)'], align='mid', color=['#d65f5f', '#5fba7d'])
# Mejora media de todos los items
# ======================================================================================
results[['improvement', 'improvement_(%)']].agg(['mean', 'min', 'max'])
# Número de series con mejora positiva y negativa
# ======================================================================================
pd.Series(np.where(results['improvement_(%)'] < 0, 'negative', 'positive')).value_counts()
El modelo global logra una mejora media del 6,6% en comparación con el uso de un modelo individual para cada serie. Para todas las series, el error de predicción evaluado mediante backtesting es menor cuando se utiliza el modelo global. Este caso de uso demuestra que un modelo multiserie puede tener ventajas sobre varios modelos individuales a la hora de predecir series temporales que siguen una dinámica similar. Además de las mejoras potenciales en la predicción, también es importante tener en cuenta el beneficio de tener un único modelo que mantener y la velocidad de entrenamiento y predicción.
⚠ Warning
Esta comparación se ha realizado sin optimizar los hiperparámetros del modelo. Consulte la sección Ajuste de hiperparámetros y selección de lags para comprobar que las conclusiones se mantienen cuando los modelos se ajustan con la mejor combinación de hiperparámetros y lags.Series de diferente longitud y distintas variables exógenas¶
En escenarios en los que se tienen que modelar múltiples series, es habitual que las series tengan longitudes distintas debido a diferencias en los momentos de inicio del registro de los datos. Para hacer frente a este escenario, la clase ForecasterAutoregMultiSeries permite modelizar simultáneamente series temporales de distintas longitudes y con distintas variables exógenas.
- Cuando las series modeladas tienen longitudes diferentes, deben almacenarse en un diccionario Python. Las claves del diccionario son los nombres de las series y los valores son las propias series. Todas las series deben ser del tipo
pandas.Series, tener un índicedatetimey tener la misma frecuencia.
| Series values | Permitido |
|---|---|
[NaN, NaN, NaN, NaN, 4, 5, 6, 7, 8, 9] |
✔️ |
[0, 1, 2, 3, 4, 5, 6, 7, 8, NaN] |
✔️ |
[0, 1, 2, 3, 4, NaN, 6, 7, 8, 9] |
✔️ |
[NaN, NaN, 2, 3, 4, NaN, 6, 7, 8, 9] |
✔️ |
- Cuando se utilizan variables exógenas diferentes para cada serie o cuando las variables exógenas son las mismas pero tienen valores diferentes para cada serie, deben almacenarse en un diccionario. Las claves del diccionario son los nombres de las series y los valores son las propias variables exógenas. Todas las variables exógenas deben ser de tipo
pandas.DataFrameopandas.Series.
Datos¶
Los datos de este ejemplo están almacenados en "formato largo" en un único DataFrame. La columna series_id identifica la serie a la que pertenece cada observación. La columna timestamp contiene la fecha de la observación, y la columna value contiene el valor de la serie en esa fecha. Cada serie temporal tiene una longitud diferente.
Las variables exógenas se almacenan en un DataFrame separado, también en "formato largo". La columna series_id identifica la serie a la que pertenece cada observación. La columna timestamp contiene la fecha de la observación, y las columnas restantes contienen los valores de las variables exógenas en esa fecha.
# Lectura series con diferentes longitudes y variables exógenas
# ==============================================================================
series = pd.read_csv(
'https://raw.githubusercontent.com/JoaquinAmatRodrigo/skforecast-datasets/main/data/demo_multi_series.csv'
)
exog = pd.read_csv(
'https://raw.githubusercontent.com/JoaquinAmatRodrigo/skforecast-datasets/main/data/demo_multi_series_exog.csv'
)
series['timestamp'] = pd.to_datetime(series['timestamp'])
exog['timestamp'] = pd.to_datetime(exog['timestamp'])
display(series.head())
display(exog.head())
Cuando las series tienen longitudes diferentes, los datos deben transformarse en un diccionario. Las claves del diccionario son los nombres de las series y los valores son las propias series. Para ello, se utiliza la función series_long_to_dict, que toma el DataFrame en "formato largo" y devuelve un diccionario de series.
Del mismo modo, cuando las variables exógenas son diferentes (valores o variables) para cada serie, los datos deben transformarse en un diccionario. Las claves del diccionario son los nombres de las series y los valores son las propias variables exógenas. Se utiliza la función exog_long_to_dict, que toma el DataFrame en "formato largo" y devuelve un diccionario de variables exógenas.
# Transform series and exog to dictionaries
# ==============================================================================
series_dict = series_long_to_dict(
data = series,
series_id = 'series_id',
index = 'timestamp',
values = 'value',
freq = 'D'
)
exog_dict = exog_long_to_dict(
data = exog,
series_id = 'series_id',
index = 'timestamp',
freq = 'D'
)
Algunas variables exógenas se omiten en las series 1 y 3 para ilustrar que se pueden utilizar diferentes variables exógenas para cada serie.
exog_dict['id_1000'] = exog_dict['id_1000'].drop(columns=['air_temperature', 'wind_speed'])
exog_dict['id_1003'] = exog_dict['id_1003'].drop(columns=['cos_day_of_week'])
# Particiones de entrenamiento y test
# ==============================================================================
end_train = '2016-07-31 23:59:00'
series_dict_train = {k: v.loc[: end_train,] for k, v in series_dict.items()}
exog_dict_train = {k: v.loc[: end_train,] for k, v in exog_dict.items()}
series_dict_test = {k: v.loc[end_train:,] for k, v in series_dict.items()}
exog_dict_test = {k: v.loc[end_train:,] for k, v in exog_dict.items()}
# Gráfico series
# ==============================================================================
set_dark_theme()
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
fig, axs = plt.subplots(5, 1, figsize=(8, 4), sharex=True)
for i, s in enumerate(series_dict.values()):
axs[i].plot(s, label=s.name, color=colors[i])
axs[i].legend(loc='upper right', fontsize=8)
axs[i].tick_params(axis='both', labelsize=8)
axs[i].axvline(pd.to_datetime(end_train) , color='white', linestyle='--', linewidth=1)
# Descripción de cada serie
# ==============================================================================
for k in series_dict.keys():
print(f"{k}:")
try:
print(
f"\tTrain: len={len(series_dict_train[k])}, {series_dict_train[k].index[0]}"
f" --- {series_dict_train[k].index[-1]}"
)
except:
print(f"\tTrain: len=0")
try:
print(
f"\tTest : len={len(series_dict_test[k])}, {series_dict_test[k].index[0]}"
f" --- {series_dict_test[k].index[-1]}"
)
except:
print(f"\tTest : len=0")
# Variables exógenas de cada serie
# ==============================================================================
for k in series_dict.keys():
print(f"{k}:")
try:
print(f"\t{exog_dict[k].columns.to_list()}")
except:
print(f"\tNo variables exógenas")
Modelo global: Forecaster multiseries¶
# Fit forecaster
# ==============================================================================
regressor = HistGradientBoostingRegressor(random_state=123, max_depth=5)
forecaster = ForecasterAutoregMultiSeries(
regressor = regressor,
lags = 14,
encoding = "ordinal",
dropna_from_series = False
)
forecaster.fit(
series = series_dict_train,
exog = exog_dict_train,
suppress_warnings = True
)
forecaster
predicciones = forecaster.predict(steps=5, exog=exog_dict_test, suppress_warnings=True)
predicciones
Backtesting¶
# Backtesting
# ==============================================================================
forecaster = ForecasterAutoregMultiSeries(
regressor=regressor, lags=14, encoding="ordinal", dropna_from_series=False
)
metrics_levels, backtest_predictions = backtesting_forecaster_multiseries(
forecaster=forecaster,
series=series_dict,
exog=exog_dict,
steps=24,
metric="mean_absolute_error",
add_aggregated_metric=False,
initial_train_size=len(series_dict_train["id_1000"]),
fixed_train_size=True,
gap=0,
allow_incomplete_fold=True,
refit=False,
n_jobs="auto",
verbose=True,
show_progress=True,
suppress_warnings=True,
)
display(metrics_levels)
display(backtest_predictions)
# Gráfico predicciones backtesting
# ==============================================================================
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
fig, axs = plt.subplots(5, 1, figsize=(8, 4), sharex=True)
for i, s in enumerate(series_dict.keys()):
axs[i].plot(series_dict[s], label=series_dict[s].name, color=colors[i])
axs[i].axvline(pd.to_datetime(end_train) , color='white', linestyle='--', linewidth=1)
try:
axs[i].plot(backtest_predictions[s], label='prediction', color="white")
except:
pass
axs[i].legend(loc='upper left', fontsize=8)
axs[i].tick_params(axis='both', labelsize=8)
Al permitir la modelización de series temporales de diferentes longitudes y con diferentes variables exógenas, la clase ForecasterAutoregMultiSeries proporciona una herramienta flexible y potente para utilizar toda la información disponible para entrenar los modelos.
Optimización de hiperparámetros (tuning) y selección de lags¶
En caso 1, la comparación entre forecaster se ha realizado sin optimizar los hiperparámetros de los regresores. Para una comparación justa, se utiliza una estrategia de grid search con el fin de seleccionar la mejor configuración para cada forecaster. Véase más información en hyperparameter tuning and lags selection.
⚠ Warning
La sección siguiente puede requerir un tiempo de ejecución considerable (alrededor de 45 minutos). Siéntase libre de seleccionar sólo un subconjunto de items para acelerar la ejecución.# Búsqueda de hiperparámetros y backtesting de un modelo para cada item
# ======================================================================================
with open(os.devnull, 'w') as devnull: # Ocultar prints
sys.stdout = devnull
items = []
mae_values = []
def search_space(trial):
search_space = {
'lags' : trial.suggest_categorical('lags', [7, 14]),
'max_iter' : trial.suggest_int('max_iter', 100, 500),
'max_depth' : trial.suggest_int('max_depth', 5, 10),
'learning_rate' : trial.suggest_float('learning_rate', 0.01, 0.1)
}
return search_space
for item in tqdm(data.columns):
forecaster = ForecasterAutoreg(
regressor = HistGradientBoostingRegressor(random_state=123),
lags = 14,
transformer_y = StandardScaler()
)
results_bayesian = bayesian_search_forecaster(
forecaster = forecaster,
y = data.loc[:end_val, item],
search_space = search_space,
n_trials = 20,
steps = 7,
metric = 'mean_absolute_error',
initial_train_size = len(data_train),
refit = False,
fixed_train_size = False,
return_best = True,
verbose = False,
show_progress = False
)
metric, preds = backtesting_forecaster(
forecaster = forecaster,
y = data[item],
initial_train_size = len(data_train) + len(data_val),
steps = 7,
metric = 'mean_absolute_error',
refit = False,
fixed_train_size = False,
verbose = False,
show_progress = False
)
items.append(item)
mae_values.append(metric.at[0, 'mean_absolute_error'])
uni_series_mae = pd.Series(
data = mae_values,
index = items,
name = 'uni_series_mae'
)
sys.stdout = sys.__stdout__
def search_space(trial):
search_space = {
'lags' : trial.suggest_categorical('lags', [7, 14]),
'max_iter' : trial.suggest_int('max_iter', 100, 500),
'max_depth' : trial.suggest_int('max_depth', 5, 10),
'learning_rate' : trial.suggest_float('learning_rate', 0.01, 0.1)
}
return search_space
forecaster_ms = ForecasterAutoregMultiSeries(
regressor = HistGradientBoostingRegressor(random_state=123),
lags = 14,
transformer_series = StandardScaler(),
encoding = 'ordinal'
)
results_bayesian_ms = bayesian_search_forecaster_multiseries(
forecaster = forecaster_ms,
series = data.loc[:end_val, :],
levels = None, # Si es None se seleccionan todos los niveles
search_space = search_space,
n_trials = 20,
steps = 7,
metric = 'mean_absolute_error',
initial_train_size = len(data_train),
refit = False,
fixed_train_size = False,
return_best = True,
verbose = False,
show_progress = False
)
multi_series_mae, predictions_ms = backtesting_forecaster_multiseries(
forecaster = forecaster_ms,
series = data,
levels = None, # Si es None se seleccionan todos los niveles
steps = 7,
metric = 'mean_absolute_error',
add_aggregated_metric = False,
initial_train_size = len(data_train) + len(data_val),
refit = False,
fixed_train_size = False,
verbose = False
)
# Diferencia de la métrica de backtesting para cada item
# ======================================================================================
multi_series_mae = multi_series_mae.set_index('levels')
multi_series_mae.columns = ['multi_series_mae']
results = pd.concat((uni_series_mae, multi_series_mae), axis = 1)
results['improvement'] = results.eval('uni_series_mae - multi_series_mae')
results['improvement_(%)'] = 100 * results.eval('(uni_series_mae - multi_series_mae) / uni_series_mae')
results = results.round(2)
# Mejora media de todos los items
# ======================================================================================
results[['improvement', 'improvement_(%)']].agg(['mean', 'min', 'max'])
# Número de series con mejora positiva y negativa
# ======================================================================================
pd.Series(np.where(results['improvement_(%)'] < 0, 'negative', 'positive')).value_counts()
Tras identificar la combinación de lags e hiperparámetros que logran el mejor rendimiento predictivo para cada forecaster, un número superior de modelos univariantes han logrado una mayor capacidad predictiva al generalizar mejor sus propios datos (un item). Aun así, el modelo multiserie proporciona mejores resultados para la mayoría de los items.
Selección de predictores¶
La selección de predictores es el proceso de seleccionar un subconjunto de predictores relevantes (variables) para su uso en la construcción del modelo. Las técnicas de selección de predictores se utilizan por varias razones: para simplificar los modelos y hacerlos más fáciles de interpretar, para reducir el tiempo de entrenamiento, para evitar los problemas de dimensionalidad, para mejorar la generalización reduciendo el sobreajuste (formalmente, la reducción de la varianza), entre otros.
Skforecast es compatible con los métodos de selección implementados en scikit-learn. Existen varios métodos de selección de características, pero los más comunes son:
Recursive feature elimination (RFE)
Sequential Feature Selection (SFS)
Feature selection based on threshold (SelectFromModel)
💡 Tip
La selección de predictores es una herramienta poderosa para mejorar el rendimiento de los modelos de machine learning. Sin embargo, es computacionalmente costosa y puede llevar tiempo. Dado que el objetivo es encontrar el mejor subconjunto de variables, no el mejor modelo, no es necesario utilizar todo el conjunto de datos o un modelo muy complejo. En su lugar, se recomienda utilizar un pequeño subconjunto de datos y un modelo simple. Una vez que se haya identificado el mejor subconjunto de variables, el modelo puede entrenarse utilizando todo el conjunto de datos y una configuración más compleja.Pesos en forecasting multiseries¶
Los pesos se utilizan para controlar la influencia que tiene cada observación en el entrenamiento del modelo. ForecasterAutoregMultiseries acepta dos tipos de pesos:
series_weightscontrola la importancia relativa de cada serie. Si una serie tiene el doble de peso que las demás, las observaciones de esa serie influyen el doble en el entrenamiento. Cuanto mayor sea el peso de una serie en relación con las demás, más se centrará el modelo en intentar aprender esa serie.weight_funccontrola la importancia relativa de cada observación en función del índice. Por ejemplo, una función que asigna un peso menor a ciertas fechas.
Si se indican los dos tipos de pesos, estos se multiplican para crear los pesos finales como se muestra en la figura. El sample_weight resultante no puede contener valores negativos.
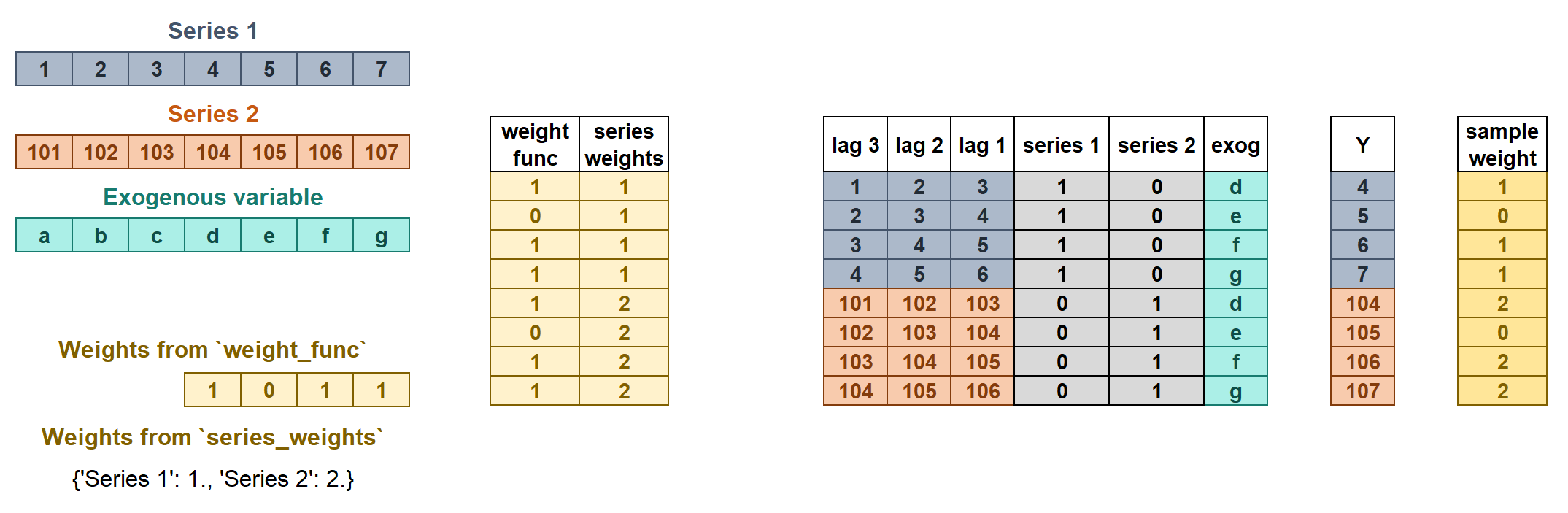
Más información sobre weights in multi-series forecasting y weighted time series forecasting con skforecast.
En este ejemplo, item_1 tiene una mayor importancia relativa entre series (pesa 3 veces más que el resto de series), y las observaciones entre '2013-12-01' y '2014-01-31' se consideran no representativas y se les aplica un peso de 0.
# Pesos en forecasting multiseries
# ======================================================================================
# Pesos de cada serie
series_weights = {'item_1': 3.} # Las series que no aparezcan en el dict tienen un peso de 1
# Pesos de cada observación (por índice)
def custom_weights(index):
"""
Devuelve 0 si el índice está entre '2013-12-01' y '2014-01-31', 1 en caso contrario.
"""
weights = np.where(
(index >= '2013-12-01') & (index <= '2014-01-31'),
0,
1
)
return weights
forecaster = ForecasterAutoregMultiSeries(
regressor = HistGradientBoostingRegressor(random_state=123),
lags = 14,
transformer_series = StandardScaler(),
transformer_exog = None,
weight_func = custom_weights,
series_weights = series_weights
)
forecaster.fit(series=data)
forecaster.predict(steps=7).head(3)
🖉 Nota
Se puede pasar un diccionario a `weight_func` para aplicar diferentes funciones a cada serie. Si una serie no se presenta en el diccionario, tendrá pesoConclusiones¶
Este caso de uso muestra como un modelo multiserie puede presentar ventajas sobre varios modelos individuales cuando se predicen series temporales con una dinámica similar. Más allá de las posibles mejoras en la predicción, también es importante tener en cuenta la ventaja de tener un solo modelo que mantener.
Información de sesión¶
import session_info
session_info.show(html=False)
Instrucciones para citar¶
¿Cómo citar este documento?
Si utilizas este documento o alguna parte de él, te agradecemos que lo cites. ¡Muchas gracias!
Modelos de forecasting globales: modelado de múltiples series temporales con machine learning por Joaquín Amat Rodrigo and Javier Escobar Ortiz, disponible con licencia Attribution-NonCommercial-ShareAlike 4.0 International (CC BY-NC-SA 4.0 DEED) en https://www.cienciadedatos.net/documentos/py44-multi-series-forecasting-skforecast-español.html
¿Cómo citar skforecast?
Si utilizas skforecast en tu investigación o publicación, te lo agradeceríamos mucho que lo cites. ¡Muchas gracias!
Zenodo:
Amat Rodrigo, Joaquin, & Escobar Ortiz, Javier. (2024). skforecast (v0.13.0). Zenodo. https://doi.org/10.5281/zenodo.8382788
APA:
Amat Rodrigo, J., & Escobar Ortiz, J. (2024). skforecast (Version 0.13.0) [Computer software]. https://doi.org/10.5281/zenodo.8382788
BibTeX:
@software{skforecast, author = {Amat Rodrigo, Joaquin and Escobar Ortiz, Javier}, title = {skforecast}, version = {0.13.0}, month = {8}, year = {2024}, license = {BSD-3-Clause}, url = {https://skforecast.org/}, doi = {10.5281/zenodo.8382788} }
¿Te ha gustado el artículo? Tu ayuda es importante
Mantener un sitio web tiene unos costes elevados, tu contribución me ayudará a seguir generando contenido divulgativo gratuito. ¡Muchísimas gracias! 😊
Este material creado por Joaquín Amat Rodrigo y Javier Escobar Ortiz tiene licencia Attribution-NonCommercial-ShareAlike 4.0 International.